Một xí nghiệp mỗi ngày sản xuất ra 2 000 sản phẩm trong đó có 39 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: “Sản phẩm lấy ta lần thứ hai bị lỗi” (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Đáp án: 0,02.
Xét các biến cố:
![]() : “Sản phẩm lấy ra lần thứ nhất bị lỗi”;
: “Sản phẩm lấy ra lần thứ nhất bị lỗi”;
![]() : “Sản phẩm lấy ra lần thứ hai bị lỗi”.
: “Sản phẩm lấy ra lần thứ hai bị lỗi”.
Khi đó, ![]() ;
; ![]() .
.
Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn 1 999 sản phẩm và trong đó có 38 sản phẩm lỗi nên ta có: ![]() , suy ra
, suy ra ![]() .
.
Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn 1 999 sản phẩm và trong đó có 39 sản phẩm lỗi nên ta có: ![]() , suy ra
, suy ra ![]() .
.
Khi đó, xác suất để sản phẩm lấy ra lần thứ hai bị lỗi là:
![]()
![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Do ![]() nên quãng đường
nên quãng đường ![]() mà xe ô tô đi được trong thời gian
mà xe ô tô đi được trong thời gian ![]() (giây) là một nguyên hàm của hàm số
(giây) là một nguyên hàm của hàm số ![]() .
.
Ta có: ![]() với
với ![]() là hằng số.
là hằng số.
Khi đó, ta gọi hàm số ![]() .
.
b) Đúng. Do ![]() nên
nên ![]() . Suy ra
. Suy ra ![]() .
.
c) Sai. Xe ô tô dừng hẳn khi ![]() hay
hay ![]() , tức là
, tức là ![]() . Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 2 giây.
. Vậy thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 2 giây.
d) Đúng. Ta có xe ô tô đang chạy với tốc độ 65 km/h ≈ 18 m/s.
Quãng đường xe ô tô còn di chuyển được kể từ lúc đạp phanh đến khi xe dừng hẳn là:
![]() (m).
(m).
Khi đó, quãng đường xe ô tô di chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là ![]() (m).
(m).
Do ![]() nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường.
nên xe ô tô đã dừng hẳn trước khi va chạm với chướng ngại vật trên đường.
Lời giải
Đáp án: 68.
Ta có: ![]() ,
, ![]() . Khi đó,
. Khi đó,
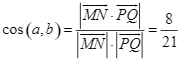 , suy ra
, suy ra ![]() .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.