Câu hỏi:
14/02/2025 3,109
Cho biểu thức: \[M = \frac{1}{{{x^2} - 2x}} \cdot \left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1.\]
a) Tìm điều kiện xác định của biểu thức \(M.\)
b) Tính giá trị của \(M\) biết \[\left| {4 - x} \right| = 2.\]
c) Tìm \[x\] để \(M\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
Cho biểu thức: \[M = \frac{1}{{{x^2} - 2x}} \cdot \left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1.\]
a) Tìm điều kiện xác định của biểu thức \(M.\)
b) Tính giá trị của \(M\) biết \[\left| {4 - x} \right| = 2.\]
c) Tìm \[x\] để \(M\) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Điều kiện xác định của biểu thức \(M\) là \(\left\{ \begin{array}{l}{x^2} - 2x \ne 0\\x \ne 0\end{array} \right.,\) hay \(\left\{ \begin{array}{l}x\left( {x - 2} \right) \ne 0\\x \ne 0\end{array} \right..\)
Khi đó \(\left\{ \begin{array}{l}x \ne 0\\x - 2 \ne 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}x \ne 0\\x \ne 2\end{array} \right..\)
Vậy điều kiện xác định của biểu thức \(M\) là \(x \ne 0\) và \(x \ne 2\).
b) Với \(x \ne 0\) và \(x \ne 2,\) ta có:
\[M = \frac{1}{{{x^2} - 2x}} \cdot \left( {\frac{{{x^2} + 4}}{x} - 4} \right) + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \left( {\frac{{{x^2} + 4}}{x} - \frac{{4x}}{x}} \right) + 1\]
\[ = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{x^2} + 4 - 4x}}{x} + 1 = \frac{1}{{x\left( {x - 2} \right)}} \cdot \frac{{{{\left( {x - 2} \right)}^2}}}{x} + 1\]
\[ = \frac{{x - 2}}{{{x^2}}} + \frac{{{x^2}}}{{{x^2}}} = \frac{{{x^2} + x - 2}}{{{x^2}}}.\]
Vậy với \(x \ne 0\) và \(x \ne 2,\) thì \(M = \frac{{{x^2} + x - 2}}{{{x^2}}}.\)
Ta có \[\left| {4 - x} \right| = 2\]
|
Trường hợp 1. \[4 - x = 2\] \(x = 2\) (không thoả mãn). |
Trường hợp 1. \[4 - x = - 2\] \(x = 6\) (thoả mãn). |
Thay \[x = 6\] vào biểu thức \(M = \frac{{{x^2} + x - 2}}{{{x^2}}},\) ta được: \[M = \frac{{{6^2} + 6 - 2}}{{{6^2}}} = \frac{{36 + 6 - 2}}{{36}} = \frac{{10}}{9}.\]
Vậy \(M = \frac{{10}}{9}\) khi \[\left| {4 - x} \right| = 2.\]
c) Với \(x \ne 0\) và \(x \ne 2,\) ta có \[M = \frac{{{x^2} + x - 2}}{{{x^2}}} = 1 + \frac{1}{x} - \frac{2}{{{x^2}}}.\]
Đặt \[\frac{1}{x} = t\,\,\,\left( {t \ne 0;\,\,t \ne \frac{1}{2}} \right),\] khi đó:
\[M = 1 + t - 2{t^2} = - 2\left( {{t^2} - \frac{1}{2}t - \frac{1}{2}} \right) = - 2\left( {{t^2} - 2 \cdot t \cdot \frac{1}{4} + \frac{1}{{16}} - \frac{1}{2} - \frac{1}{{16}}} \right)\]
\[ = - 2\left[ {{{\left( {t - \frac{1}{4}} \right)}^2} - \frac{9}{{16}}} \right] = \frac{9}{8} - 2{\left( {t - \frac{1}{4}} \right)^2}.\]
Vì \[{\left( {t - \frac{1}{4}} \right)^2} \ge 0\] nên \[ - 2{\left( {t - \frac{1}{4}} \right)^2} \le 0,\] do đó \[P \le \frac{9}{8}.\]
Dấu đẳng thức xảy ra khi tức là \[t = \frac{1}{4}\] (thoả mãn).
Với \(t = \frac{1}{4},\) ta có \[\frac{1}{x} = \frac{1}{4},\] suy ra \[x = 4.\]
Vậy giá trị lớn nhất củ\[t - \frac{1}{4} = 0,\]a \[M\] là \[\frac{9}{8}\] khi \[x = 4.\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
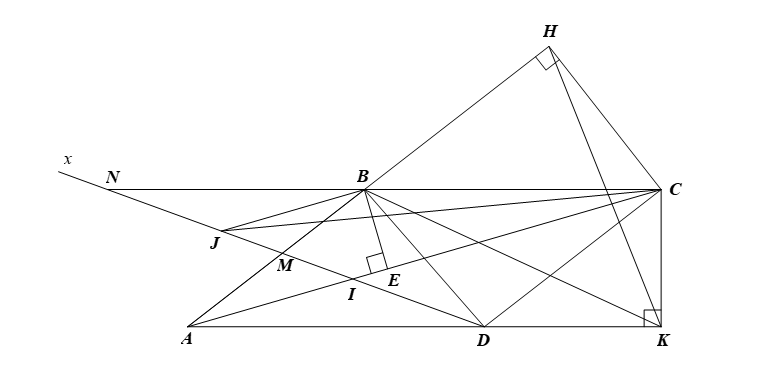
a) Ta có \(ABCD\) là hình bình hành nên \(\widehat {ABC} = \widehat {ADC}\) \(\left( 1 \right)\) (tính chất hình bình hành)
Mà \(\widehat {HBC} = 180^\circ - \widehat {ABC}\) \(\left( 2 \right)\) (hai góc kề bù)
\(\widehat {KDC} = 180^\circ - \widehat {ADC}\) \(\left( 3 \right)\) (hai góc kề bù)
Từ \(\left( 1 \right)\), \(\left( 2 \right)\), \(\left( 3 \right)\) suy ra \(\widehat {HBC} = \widehat {KDC}.\)
Xét \(\Delta CHB\) và \(\Delta CKD\) có:
\(\widehat {BHC} = \widehat {DKC} = 90^\circ \) và \(\widehat {HBC} = \widehat {KDC}\)
Do đó (g.g).
Suy ra \(\frac{{CH}}{{CK}} = \frac{{CB}}{{CD}}\) (tỉ số cạnh tương ứng), hay \(\frac{{CH}}{{CB}} = \frac{{CK}}{{CD}}\) (tính chất tỉ lệ thức).
b) Ta có \(\widehat {ABC}\) là góc ngoài của \(\Delta BHC\) nên \(\widehat {ABC} = \widehat {BHC} + \widehat {BCH} = 90^\circ + \widehat {BCH}\)\(\left( 4 \right)\)
Vì \(ABCD\) là hình bình hành nên \(BC\,{\rm{//}}\,AD\) và \(AB = CD\) (tính chất hình bình hành)
Mà \(CK \bot AD\) nên \(CK \bot BC\) nên \(\widehat {BCK} = 90^\circ .\)
Do đó \(\widehat {KCH} = \widehat {BCK} + \widehat {BCH} = 90^\circ + \widehat {BCH}\) \(\left( 5 \right)\)
Từ \(\left( 4 \right)\) và \(\left( 5 \right)\) suy ra \(\widehat {ABC} = \widehat {KCH}.\)
Theo câu a, \(\frac{{CH}}{{CB}} = \frac{{CK}}{{CD}}\) mà \(AB = CD\) nên \(\frac{{CH}}{{CB}} = \frac{{CK}}{{BA}}.\)
Xét \(\Delta CHK\) và \(\Delta BCA\) có: \(\widehat {KCH} = \widehat {ABC}\) và \(\frac{{CH}}{{CB}} = \frac{{CK}}{{BA}}\)
Do đó (c.g.c).
c) Kẻ \(BE \bot AC\) tại \(E\) \(\left( {E \in AC} \right).\)
Xét \(\Delta AEB\) và \(\Delta AHC\) có: \(\widehat {AEB} = \widehat {AHC} = 90^\circ \) và \(\widehat {HAC}\) là góc chung.
Do đó (g.g).
Suy ra \(\frac{{AB}}{{AC}} = \frac{{AE}}{{AH}}\) (tỉ số cạnh tương ứng) nên \(AB \cdot AH = AC \cdot AE\)\(\left( 6 \right)\)
Xét \(\Delta BCE\) và \(\Delta CAK\) có:
\(\widehat {BEC} = \widehat {CKA} = 90^\circ \) và \(\widehat {BCE} = \widehat {CAK}\) (hai góc so le trong, \(BC\,{\rm{//}}\,DA)\)
Do đó (g.g).
Suy ra \(\frac{{BC}}{{CA}} = \frac{{CE}}{{AK}}\) (tỉ số cạnh tương ứng) nên \(BC \cdot AK = AC \cdot CE\)
Mà \(BC = AD\) nên \(AD \cdot AK = AC \cdot CE\) \(\left( 7 \right)\)
Từ \(\left( 6 \right)\) và \(\left( 7 \right)\) suy ra: \(AB \cdot AH + AD \cdot AK = AC \cdot AE + AC \cdot CE\)
Hay \(AB \cdot AH + AD \cdot AK = AC\left( {AE + CE} \right) = A{C^2}.\)
d) Do \(ABCD\) là hình bình hành nên \(AB\,{\rm{//}}\,CD;\;AD\,{\rm{//}}\,BC\) (tính chất hình bình hành)
Hay \(AM\,{\rm{//}}\,CD;\;AD\,{\rm{//}}\,NC.\)
Vì \(AD\,{\rm{//}}\,NC\) nên do đó \(\frac{{IN}}{{ID}} = \frac{{IC}}{{IA}}\) (tỉ số cạnh tương ứng) \(\left( 8 \right)\)
Vì \(AM\,{\rm{//}}\,DC\) nên do đó \(\frac{{ID}}{{IM}} = \frac{{IC}}{{IA}}\) (tỉ số cạnh tương ứng) \(\left( 9 \right)\)
Từ \(\left( 8 \right)\) và \(\left( 9 \right)\) suy ra \(\frac{{IN}}{{ID}} = \frac{{ID}}{{IM}},\) nên \(IM \cdot IN = I{D^2}.\)
Lời giải
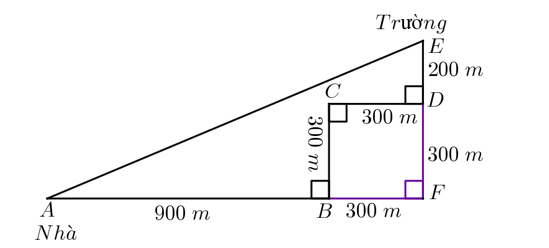
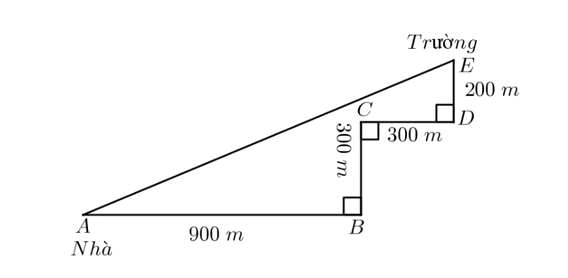
Gọi \(F\) là giao điểm của \(AB\) và \(ED.\)
Quan sát đường đi của bạn An theo hình vẽ thì đó là tứ giác \(BCDF,\) tứ giác này có \(\widehat {B\,} = \widehat {C\,} = \widehat {D\,} = 90^\circ \) nên là hình chữ nhật.
Mà \(CD = CB = 300\) m nên hình chữ nhật \(BCDF\) là hình vuông.
Do đó \(BC = CD = DF = FB = 300\) (m) và \(\widehat {BFD} = 90^\circ .\)
Ta có \(AF = AB + BF = 900 + 300 = 1\,\,200\) (m); \(EF = FD + DE = 300 + 200 = 500\) (m).
Áp dụng định lí Pythagore cho \(\Delta AEF\) vuông tại \(F\) ta có:
\(A{E^2} = A{F^2} + E{F^2}\)\( = 1\,\,{200^2} + {500^2} = 1{\rm{ }}690{\rm{ }}000.\)
Suy ra \(AE = \sqrt {1{\rm{ }}690{\rm{ }}000} = 1\,\,300\) (m) \( = 1,3\) (km).
Thời gian đi hết quãng đường \(AE\) là: \(\frac{{1,3}}{{13}} = 0,1\) (giờ) \( = 6\) (phút).
Vậy bạn An đi từ nhà đến trường (bằng xe đạp điện) là lúc \(7\) giờ \(6\) phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận