Quảng cáo
Trả lời:
Đáp án: \(8,1\)
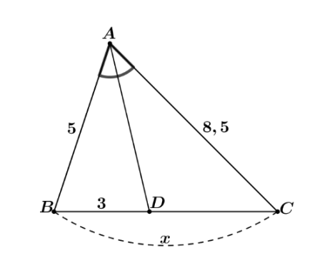
Xét tam giác \(ABC\) có \(AD\) là phân giác của \(\widehat {BAC}\) (do \(\widehat {BAD} = \widehat {CAD}\)) nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}\) hay \(\frac{{DB}}{{AB}} = \frac{{DC}}{{AC}}.\)
Do đó, \(\frac{3}{5} = \frac{{DC}}{{8,5}}\) suy ra \(DC = \frac{{8,5.3}}{5} = 5,1\).
Khi đó, \(x = BC = BD + DC = 3 + 5,1 = 8,1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: a) Đ b) S c) Đ d) Đ
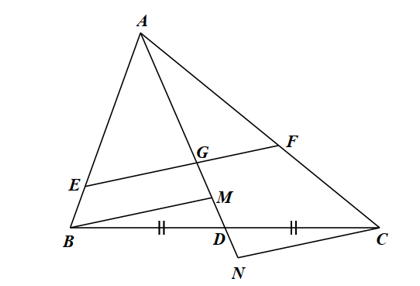
a) Xét \(\Delta ABC\) có \(EG\parallel BM\), theo định lí Thalès ta có: \(\frac{{BE}}{{AE}} = \frac{{MG}}{{AG}}\).
b) Xét \(\Delta DCN\) có \(BM\parallel CN\), theo định lí Thalès ta có: \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}}\).
c) Có \(D\) là trung điểm của \(BC\) (do \(AD\) là trung tuyến của tam giác) nên \(DB = DC\).
Do đó, \(\frac{{DN}}{{MD}} = \frac{{DC}}{{DB}} = 1\) nên \(DM = DN\).
Suy ra \(GM + GN = GM + GM + MN = 2GM + 2MD = 2GD\).
Lại có \(G\) là trọng tâm \(\Delta ABC\) nên \(AG = 2GD\).
Xét \(\Delta ACN\) có \(FG\parallel CN\), theo định lí Thalès ta có: \(\frac{{CF}}{{AF}} = \frac{{GN}}{{AG}}\).
Suy ra \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = \frac{{MG}}{{AG}} + \frac{{GN}}{{AG}} = \frac{{GM + GN}}{{AG}} = \frac{{2GD}}{{2GD}} = 1\).
Do đó, \(\frac{{BE}}{{AE}} + \frac{{CF}}{{AF}} = 1\).
d) Xét \(\Delta ABC\) có \(EG\parallel BM\), theo định lí Thalès ta có: \(\frac{{AB}}{{AE}} = \frac{{AM}}{{AG}}\).
Xét \(\Delta ACN\) có \(FG\parallel CN\), theo định lí Thalès ta có: \(\frac{{AC}}{{AF}} = \frac{{AN}}{{AG}}\).
Suy ra \(\frac{{AB}}{{AE}} + \frac{{AC}}{{AF}} = \frac{{AM}}{{AG}} + \frac{{AN}}{{AG}} = \frac{{AM + AN}}{{AG}} = \frac{{AG + GM + AG + GM + MN}}{{AG}}\)
\( = \frac{{2AG + 2GM + 2MD}}{{AG}} = \frac{{2AG + 2\left( {GM + MD} \right)}}{{AG}} = \frac{{2AG + 2GD}}{{AG}} = \frac{{2AG + 2.\frac{1}{2}AG}}{{AG}} = \frac{{3AG}}{{AG}} = 3\).
Vậy \(\frac{{AB}}{{AE}} + \frac{{CA}}{{AF}} = 3\).
Lời giải
a) Nhận thấy hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) có hệ số \(2 \ne - 1\) nên chúng cắt nhau.
Xét phương trình hoành độ giao điểm, ta có:
\(2x - 1 = - x + 2\) suy ra \(3x = 3\) nên \(x = 1\).
Thay \(x = 1\) vào đường thẳng \(\left( {{d_1}} \right)\), ta có \(y = 1.\)
Vậy ta có giao điểm \(I\left( {1;1} \right)\).
b) Gọi phương trình đường thẳng \(\left( {{d_3}} \right)\) là: \(y = ax + b\)
Theo đề, đường thẳng \(\left( {{d_3}} \right)\) song song với \(y = \frac{1}{2}x + 9\) nên có hệ số \(a = \frac{1}{2}\).
Vì \(\left( {{d_3}} \right)\) đi qua \(I\) nên ta có \(1 = \frac{1}{2}.1 + b\) suy ra \(b = \frac{1}{2}\).
Vậy \(\left( {{d_3}} \right):y = \frac{1}{2}a + \frac{1}{2}.\)
Câu 3
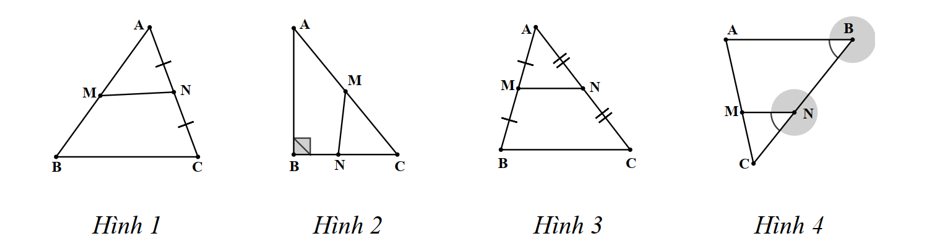
A. Hình 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.