Câu hỏi:
15/02/2025 147
Cho hình thang \(ABCD\) có \(AB\parallel CD\) và \(AB < CD\). Đường thẳng song song với đáy \(AB\) cắt các cạnh bên \(AD,BC\) theo thứ tự tại \(M,N\).
a) \(\frac{{EA}}{{AD}} = \frac{{EB}}{{BC}}.\)
b) \(\frac{{EA}}{{AM}} = \frac{{BN}}{{BE}}.\)
c) \(\frac{{MA}}{{MD}} = \frac{{NB}}{{NC}}.\)
d) \(\frac{{MD}}{{DA}} = \frac{{BC}}{{NC}}.\)
Cho hình thang \(ABCD\) có \(AB\parallel CD\) và \(AB < CD\). Đường thẳng song song với đáy \(AB\) cắt các cạnh bên \(AD,BC\) theo thứ tự tại \(M,N\).
a) \(\frac{{EA}}{{AD}} = \frac{{EB}}{{BC}}.\)
b) \(\frac{{EA}}{{AM}} = \frac{{BN}}{{BE}}.\)
c) \(\frac{{MA}}{{MD}} = \frac{{NB}}{{NC}}.\)
d) \(\frac{{MD}}{{DA}} = \frac{{BC}}{{NC}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: a) Đ b) S c) Đ d) S
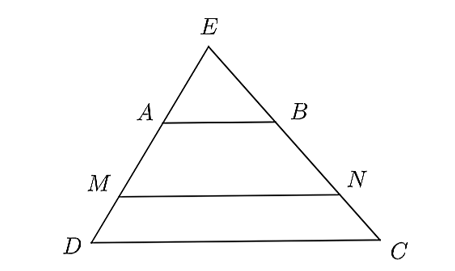
a) Vì \(AB\parallel CD\) nên theo định lí Thalès, ta có: \(\frac{{AE}}{{AD}} = \frac{{EB}}{{BC}}\).
b) Vì \(AB\parallel MN\) nên theo định lí Thalès, ta có: \(\frac{{AE}}{{AM}} = \frac{{BE}}{{BN}}\).
c) Từ a) và b) ta có: \(\frac{{AM}}{{AD}} = \frac{{BN}}{{BC}}\) hay \(\frac{{AM}}{{BN}} = \frac{{AD}}{{BC}}\).
Lại có \(\frac{{AM}}{{BN}} = \frac{{AD}}{{BC}} = \frac{{AE}}{{BE}}\) nên theo tính chất của tỉ lệ thức suy ra \(\frac{{AM}}{{BN}} = \frac{{AD - AM}}{{BC - BN}} = \frac{{MD}}{{NC}}\).
Do đó, \(\frac{{AM}}{{BN}} = \frac{{MD}}{{NC}}\) hay \(\frac{{AM}}{{DM}} = \frac{{BN}}{{BC}}\).
d) Từ c) ta có: \(\frac{{AM}}{{BN}} = \frac{{MD}}{{NC}} = \frac{{AD}}{{BC}}\) nên theo tính chất của tỉ lệ thức, ta có:
\(\frac{{MD}}{{NC}} = \frac{{AM + MD}}{{BN + NC}} = \frac{{AD}}{{BC}}\) hay \(\frac{{DM}}{{NC}} = \frac{{AD}}{{BC}}\) hay \(\frac{{DM}}{{AD}} = \frac{{NC}}{{BC}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(3\)
Để \(\left( {{m^2} - 9} \right)x = m - 3\) có vô số nghiệm thì \({m^2} - 9 = 0\) và \(m - 3 = 0\).
• Xét \({m^2} - 9 = 0\), ta có: \(\left( {m - 3} \right)\left( {m + 3} \right) = 0\), tức là \(m - 3 = 0\) hoặc \(m + 3 = 0\) nên \(m = 3\) hoặc \(m = - 3.\)
• Xét \(m - 3 = 0\) khi \(m = 3\).
Kết hợp điều kiện ta được \(m = 3\).
Vậy giá trị thỏa mãn yêu cầu bài toán là \(m = 3\).
Lời giải
Đáp án: \( - 1\)
Xét phương trình hoành độ giao điểm của \({d_1}\) và \({d_2}\), ta có:
\(x - 1 = - x + 1\) suy ra \(2x = 2\) và \(x = 1\).
Với \(x = 1\) thay vào \({d_1}\) được \(y = 0\).
Suy ra điểm \(A\left( {1;0} \right)\) là giao của hai đường thẳng \({d_1}\) và \({d_2}\).
Để để hai đường thẳng \({d_1}\) cắt \({d_2}\) tại một điểm thuộc đường thẳng \({d_3}\) tức là ba đường thẳng đồng quy.
Do đó, \(A\left( {1;0} \right) \in {d_3}\).
Thay \(x = 1\), \(y = 0\) vào \({d_3}\), ta được:
\( - 3a + 2a - 1 = 0\) hay \( - a - 1 = 0\) suy ra \(a = - 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận