Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng 500 nghìn đồng một giờ.
a) Viết công thức của hàm số biểu thị tổng chi phí \[y\] (nghìn đồng) để thuê một chiếc thuyền du lịch trong \[x\] (giờ).
b) Vẽ đồ thị của hàm số thu được ở câu a để tìm tổng chi phí cho một lần thuê trong 3 giờ. Giao điểm của đồ thị với trục tung biểu thị điều gì?
Một công ty cho thuê thuyền du lịch tính phí thuê thuyền là 1 triệu đồng, ngoài ra tính phí sử dụng 500 nghìn đồng một giờ.
a) Viết công thức của hàm số biểu thị tổng chi phí \[y\] (nghìn đồng) để thuê một chiếc thuyền du lịch trong \[x\] (giờ).
b) Vẽ đồ thị của hàm số thu được ở câu a để tìm tổng chi phí cho một lần thuê trong 3 giờ. Giao điểm của đồ thị với trục tung biểu thị điều gì?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) 1 triệu đồng \[ = 1{\rm{ }}000\] nghìn đồng.
Hàm số biểu thị tổng chi phí \[y\] (nghìn đồng) để thuê một chiếc thuyền du lịch trong \[x\] (giờ) là: \[y = 1{\rm{ }}000 + 500x\] (nghìn đồng).
|
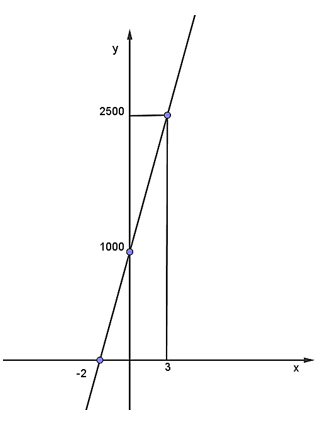
b) Đồ thị hàm số \[y = 1{\rm{ }}000 + 500x\] đi qua hai điểm \[\left( {--2;0} \right)\] và \[\left( {0;1{\rm{ }}000} \right)\] nên đồ thị hàm số được vẽ như hình bên. Tổng chi phí cho một lần thuê trong \[x = 3\] giờ tương ứng với điểm \[y = 2{\rm{ }}500\] nghìn đồng = 2 triệu 500 nghìn đồng. Giao điểm của đồ thị với trục tung là điểm \[\left( {0;{\rm{ }}1{\rm{ }}000} \right).\] Giao điểm này biểu thị chi phí cố định khi thuê thuyền, dù không sử dụng giờ nào (tức là \[x = 0)\] vẫn phải trả phí 1 triệu đồng này, nếu đặt thuê. |
 |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Vì \(ABCD\) là hình thang có hai đáy \(AB\) và \(CD\) nên \(AB\,{\rm{//}}\,CD.\) Vì \(AB\,{\rm{//}}\,DM\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả định lí Thalès ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}}.\) \(\left( 1 \right)\) Vì \(AB\,{\rm{//}}\,MC\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả |
 |
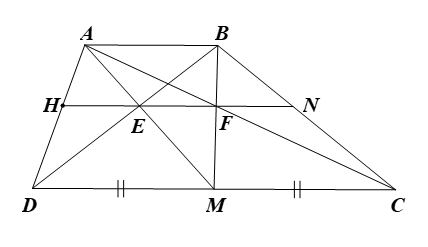định lí Thalès ta có \(\frac{{BF}}{{FM}} = \frac{{AB}}{{MC}}.\) \(\left( 2 \right)\)
Lại có \(M\) là trung điểm của \(CD\) nên \(DM = MC.\) \(\left( 3 \right)\)
Từ \(\left( 1 \right),\) \(\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\frac{{AE}}{{EM}} = \frac{{BF}}{{FM}},\) theo định lí Thalès đảo ta có \(EF\,{\rm{//}}\,AB.\)
b) Xét \(\Delta ADM\) có \(HE\,{\rm{//}}\,DM,\) theo hệ quả định lí Thalès ta có \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}}.\)
Xét \(\Delta AMC\) có \(EF\,{\rm{//}}\,MC,\) theo hệ quả định lí Thalès ta có \[\frac{{EF}}{{MC}} = \frac{{AE}}{{AM}}.\]
Do đó \(\frac{{HE}}{{DM}} = \frac{{EF}}{{MC}},\) mà \(DM = MC\) nên \(HE = EF.\)
Chứng minh tương tự ta cũng có \(EF = FN.\) Suy ra \(HE = EF = FN.\)
c) Vì \(M\) là trung điểm của \(CD\) nên \(DM = MC = \frac{1}{2}CD = \frac{1}{2} \cdot 12 = 6{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Theo câu a, ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}} = \frac{{7,5}}{6} = \frac{5}{4}.\) Suy ra \(\frac{{AE}}{5} = \frac{{EM}}{4}.\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AE}}{5} = \frac{{EM}}{4} = \frac{{AE + EM}}{{5 + 4}} = \frac{{AM}}{9}.\)
Do đó \(\frac{{AE}}{{AM}} = \frac{5}{9}.\)
Mà theo câu b, \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}} = \frac{5}{9}.\)
Suy ra \(HE = \frac{5}{9}DM = \frac{5}{9} \cdot 6 = \frac{{10}}{3}{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Vậy \(HN = 3HE = 3 \cdot \frac{{10}}{3} = 10{\rm{\;}}\left( {{\rm{cm}}} \right).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Công thức \[y\] theo \[x\] là \[y = 1200\,\,000 + \left( {x--7{\rm{ }}} \right) \cdot 100\,\,000\] (đồng)
Khi đó, \[y\] là hàm số của \[x\]. Vì mỗi giá trị của \[x\] chỉ xác định đúng một giá trị của \[y\].
b) Tổng số tiền người đó phải trả là:
\[1200\,\,000 + \left( {9--7{\rm{ }}} \right) \cdot 100\,\,000 = 1400\,\,000\] (đồng).
Vậy người đó phải trả tổng cộng \[1400\,\,000\] đồng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập