Trong giờ thực hành thí nghiệm, một học sinh thả một miếng chì có khối lượng $0,31$ kg đang ở nhiệt độ $100^\circ {\rm{C}}$ vào $0,25$ kg nước đang ở nhiệt độ $58,5^\circ {\rm{C}}.$ Biết nhiệt dung riêng của nước là $4\,\,200$ J/kg.K, nhiệt dung riêng của chì là 130 J/kg.K. gọi $t^\circ {\rm{C}}$ là nhiệt độ khi đạt trạng thái cân bằng nhiệt, ${Q_{nuoc}}$ (J) là nhiệt lượng nước thu vào để tăng nhiệt độ từ $58,5^\circ {\rm{C}}$ lên $t^\circ {\rm{C,}}$ ${Q_{chi}}$ (J) là nhiệt lượng chì tỏa ra để giảm nhiệt độ từ $100^\circ {\rm{C}}$ xuống $t^\circ {\rm{C}}{\rm{.}}$

a) Biết công thức tính nhiệt lượng thu vào/ tỏa ra là: $Q = m \cdot c \cdot \Delta t$ (J), trong đó $m$ là khối lượng của vật (kg), $c$ là nhiệt dung riêng của chất làm nên vật (J/kg.K) và $\Delta t = {t_2} - {t_1}$ là độ tăng/giảm nhiệt độ của vật $\left( {^\circ {\rm{C}}} \right)$ với ${t_1}$ là nhiệt độ ban đầu, ${t_2}$ là nhiệt độ cuối cùng. Viết công thức tính ${Q_{chi}}$ theo $t.$

b) Công thức tìm được ở câu a có phải là hàm số bậc nhất không? Nếu có, hãy tìm các hệ số $a,\,\,b$ của nó. Khi có sự cân bằng nhiệt thì nhiệt độ của nước và chì là bao nhiêu (làm tròn kết quả đến hàng đơn vị)?

Xem lời giải

Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Nhiệt lượng chì tỏa ra để giảm nhiệt độ từ $100^\circ {\rm{C}}$ xuống $t^\circ {\rm{C}}$ là:

${Q_{chi}} = 0,31 \cdot 130 \cdot \left( {100 - t} \right) = - 40,3t + 4\,\,030$ (J).

b) Công thức ${Q_{chi}} = - 40,3t + 4\,\,030$ (J) là hàm số bậc nhất với hệ số $a = - 40,3$ và $b = 4\,\,030.$

Nhiệt lượng nước thu vào để tăng nhiệt độ từ $58,5^\circ {\rm{C}}$ lên $t^\circ {\rm{C}}$ là:

${Q_{nuoc}} = 0,25 \cdot 4\,\,200 \cdot \left( {t - 58,5} \right) = 1\,\,050t - 61\,\,425$ (J).

Khi cân bằng nhiệt, nhiệt lượng tỏa ra bằng với nhiệt lượng thu vào nên ta có: ${Q_{nuoc}} = {Q_{chi}}$.

Do đó $1\,\,050t - 61\,\,425 = - 40,3t + 4\,\,030$

$1\,\,090,3t = 65\,\,455$

$t \approx 60$

Vậy nhiệt độ của nước và chì khi đạt trạng thái cân bằng nhiệt là khoảng $60^\circ {\rm{C}}.$

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa hai bên thang (như hình vẽ bên) sao cho hai chân thang rộng một khoảng là \[80{\rm{ cm}}.\] Hỏi người thợ đã làm thanh ngang đó dài bao nhiêu cm?

Xem đáp án

Lời giải

Gọi \[MN\] là thanh ngang; \[BC\] là độ rộng giữa hai bên thang.

Thanh ngang \[MN\] nằm chính giữa thang nên \[M;{\rm{ }}N\]là trung điểm \[AB\] và \[AC.\]

Suy ra \[MN\] là đường trung bình của tam giác \[ABC.\]

Suy ra $MN = \frac{1}{2}BC = \frac{1}{2}.80 = 40\,\,{\rm{(cm)}}$.

Vậy người thợ đã làm thanh ngang đó dài \[40{\rm{ cm}}.\]

Khi thiết kế một cái thang gấp, để đảm bảo an toàn người thợ đã làm thêm một thanh ngang để giữ cố định ở chính giữa (ảnh 2)

Câu 2

Cho $\Delta ABC$ có đường phân giác $AD.$

a) Giả sử $AB = 6\;{\rm{cm}},$ $BC = 10\;{\rm{cm}},$ $AC = 9\;{\rm{cm}}.$ Tính độ dài đoạn thẳng $BD.$

b) Trên tia đối của các tia $AB$ và $AC,$ lần lượt lấy các điểm $E$ và $F$ sao cho $AE = \frac{1}{3}AB,\,\,AC = 3AF.$ Chứng minh $EF\,{\rm{//}}\,BC.$

c) Qua $A,$ kẻ đường thẳng $d$ song song với $BC.$ Đường thẳng $d$ cắt $BF$ và $CE$ lần lượt tại $I$ và $K.$ Chứng minh:

i) $A$ là trung điểm của $IK.$ ii) $\frac{{FI}}{{FB}} + \frac{{CK}}{{CE}} = 1.$

Xem đáp án

Lời giải

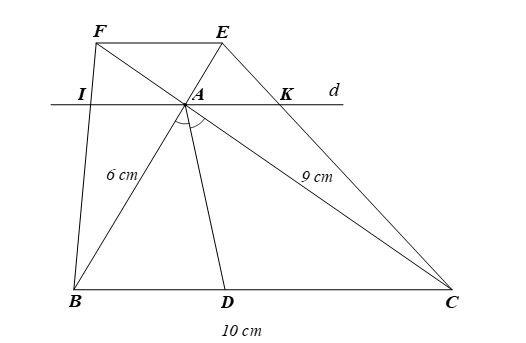
Cho tam giác ABC có đường phân giác AD a) giả sử AB= 6cm , BC = 10 cm , AC = 9 cm (ảnh 1)

a) Xét $\Delta ABC$ có $AD$ là tia phân giác của $\widehat {BAC},$ nên $\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}}$ (tính chất đường phân giác), suy ra $\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}}.$

Theo tính chất dãy tỉ số bằng nhau ta có

$\frac{{AB}}{{DB}} = \frac{{AC}}{{DC}} = \frac{{AB + AC}}{{DB + DC}} = \frac{{AB + AC}}{{BC}} = \frac{{6 + 9}}{{10}} = \frac{{15}}{{10}} = \frac{3}{2}.$

Suy ra $DB = \frac{2}{3}AB = \frac{2}{3} \cdot 6 = 4{\rm{\;cm}},\,\,DC = \frac{2}{3}AC = \frac{2}{3} \cdot 9 = 6{\rm{\;cm}}.$

b) Từ $AE = \frac{1}{3}AB$ suy ra $\frac{{AE}}{{AB}} = \frac{1}{3}.$

Từ $AC = 3AF$ suy ra $\frac{{AF}}{{AC}} = \frac{1}{3}.$

Do đó $\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}} = \frac{1}{3}.$

Theo định lí Thalès đảo ta có $EF\,{\rm{//}}\,BC.$

c) Xét $\Delta FBC$ có $IA\,{\rm{//}}\,BC$ (do $d\,{\rm{//}}\,BC)$ nên theo hệ quả định lí Thalès ta có: $\frac{{FI}}{{FB}} = \frac{{AF}}{{FC}} = \frac{{IA}}{{BC}}.\,\,\,\left( 1 \right)$

Xét $\Delta EBC$ có $AK\,{\rm{//}}\,BC$ (do $d\,{\rm{//}}\,BC)$ nên theo hệ quả định lí Thalès ta có: $\frac{{EA}}{{EB}} = \frac{{AK}}{{BC}}.\,\,\,\left( 2 \right)$

Xét $\Delta ABC$ có $EF\,{\rm{//}}\,BC$ (câu b) theo hệ quả định lí Thalès ta có: $\frac{{AE}}{{AB}} = \frac{{AF}}{{AC}} = \frac{{EF}}{{BC}},$ suy ra $\frac{{AE}}{{AE + AB}} = \frac{{AF}}{{AF + AC}},$ hay $\frac{{AE}}{{EB}} = \frac{{AF}}{{FC}}.\,\,\,\left( 3 \right)$

Từ (1), (2) và (3) suy ra $\frac{{IA}}{{BC}} = \frac{{AK}}{{BC}},$ do đó $AI = AK,$ hay $A$ là trung điểm của $IK.$

ii) Xét $\Delta EBC$ có $AK\,{\rm{//}}\,BC$ (do $d\,{\rm{//}}\,BC)$ nên theo hệ quả định lí Thalès ta có: $\frac{{CK}}{{CE}} = \frac{{CA}}{{CF}}.\,\,\,\left( 4 \right)$

Từ (1) và (4) ta có $\frac{{FI}}{{FB}} + \frac{{CK}}{{CE}} = \frac{{AF}}{{FC}} + \frac{{CA}}{{CF}} = \frac{{FC}}{{FC}} = 1.$

Vậy $\frac{{FI}}{{FB}} + \frac{{CK}}{{CE}} = 1.$

Câu 3