Câu hỏi:
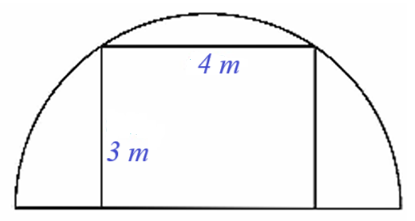
03/03/2025 250Người ta cần xây dựng một khung cổng hình chữ nhật rộng \[4{\rm{ m}}\] và cao \[3{\rm{ m,}}\] bên ngoài khung cổng được bao bởi một khung thép dạng nửa hình tròn (như hình vẽ). Chiều dài của đoạn thép dùng để làm khung nửa đường tròn đó là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp số: 60.
Gọi \[ABCD\] là khung cổng hình chữ nhật.
Vẽ hình chữ nhật \[ABEF\] (hình vẽ) và \[O\] là giao điểm của hai đường chéo \[AE,{\rm{ }}BF.\]
Khi đó ta có \[AF = 2AD = 2 \cdot 3 = 6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\]
Tam giác \[ABF\] vuông tại A, theo định lí Pythagore, ta có:
\[B{F^2} = A{F^2} + A{B^2} = {6^2} + {4^2} = 52.\]
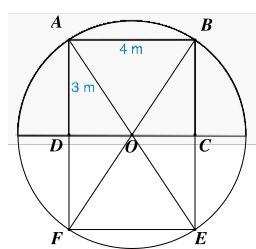
Do đó \[BF = \sqrt {52} = 2\sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Vì vậy bán kính đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[R = \frac{{BF}}{2} = \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Chu vi đường tròn ngoại tiếp hình chữ nhật \[ABEF\] là: \[C = 2\pi R = 2\pi \sqrt {13} \,\,\left( {{\rm{cm}}} \right).\]
Vậy chiều dài của đoạn thép dùng để làm khung nửa đường tròn là: \[\frac{C}{2} = \frac{{2\pi \sqrt {13} }}{2} \approx 11,33\,\,\left( {{\rm{cm}}} \right).\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một cái ly thủy tinh (như hình vẽ), phần phía trên là hình nón có chiều cao \[7\,{\rm{cm,}}\] có đáy đường tròn bán kính \[4\,\,{\rm{cm}}{\rm{.}}\] Biết trong ly đang chứa rượu với mức rượu đang cách miệng ly là \[3\,\,{\rm{cm}}.\]
a) Thể tích hình nón có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \pi {R^2}h.\)
b) Chiều cao của phần rượu có trong ly là \[4\,\,{\rm{cm}}.\]
c) Thể tích của cái ly thủy tinh là \[\frac{{28}}{3}\pi \,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}{\rm{.}}\]
d) Tỉ số giữa thể tích của phần còn lại trong ly rượu so với thể tích ly là \[\frac{4}{7}\].
Xem đáp án »
03/03/2025
12,859
Câu 2:
Phần 3. Câu hỏi trắc nghiệm trả lời ngắn
Để chở 15 tấn thiết bị phục vụ Lễ kỷ niệm 70 năm chiến thắng Điện Biên Phủ, một đội vận chuyển dự định sử dụng các xe tải loại nhỏ. Do thay đổi kế hoạch, đội vận chuyển quyết định chỉ sử dụng các xe tải loại lớn. Vì vậy, số xe sử dụng giảm đi hai xe so với dự định và mỗi xe tải loại lớn chở nhiều hơn mỗi xe tải loại nhỏ là 2 tấn. Biết mỗi xe tải cùng loại đều chở số tấn thiết bị bằng nhau. Hỏi đội vận chuyển sử dụng bao nhiêu xe tải loại lớn?
Xem đáp án »
03/03/2025
2,833
Câu 3:
B. Tự luận
1. Kết quả nhảy xa của một lớp (đơn vị mét) được cho trong bảng sau:
|
2,4 |
3,1 |
2,7 |
2,8 |
3,2 |
2,8 |
4,1 |
3,2 |
|
2,1 |
3,2 |
2,1 |
3,2 |
2,3 |
2,5 |
2,6 |
3,3 |
|
3,6 |
2,0 |
2,0 |
2,7 |
3,1 |
2,3 |
4,3 |
3,9 |
|
3,9 |
3,5 |
3,6 |
3,7 |
2,7 |
3,5 |
3,5 |
2,4 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tấn số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 5 nhóm trong đó nhóm cuối cùng cự li là từ 4,0 đến dưới 4,5 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Cho hai túi I và II mỗi túi chứa 3 tấm thẻ được đánh số \[2\,;\,\,3\,;\,\,4.\] Rút ngẫu nhiên từ mỗi túi ra 1 tấm thẻ và ghép thành số có hai chữ số với chữ số trên tấm thẻ rút từ túi I là chữ số hàng chục. Tính xác suất của biến cố “Số tạo thành là số chia hết cho 3”.
Xem đáp án »
03/03/2025
1,843
Câu 4:
Một hộp chứa 4 tấm thẻ cùng loại được đánh số 1;4;7;9 Bạn Khuê và bạn Hương lần lượt mỗi người lấy ra 1 tấm thẻ từ hộp. Tính xác suất của biến cố \(A:\) “Số ghi trên tấm thẻ của bạn Khuê nhỏ hơn số ghi trên tấm thẻ của bạn Hương” (viết kết quả dưới dạng số thập phân).
Xem đáp án »
03/03/2025
1,692
Câu 5:
A. Trắc nghiệm
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn
Giá trị của \[m\] để hàm số \[y = \left( {2 - m} \right){x^2}\,\,\left( {m \ne 2} \right)\] nghịch biến với mọi giá trị của \[x > 0\] là
Xem đáp án »
03/03/2025
951
Câu 7:
Cho bảng tần số ghép nhóm:
|
Nhóm |
\[\left[ {7\,;\,\,13} \right)\] |
\[\left[ {13\,;\,\,19} \right)\] |
\[\left[ {19\,;\,\,25} \right)\] |
\[\left[ {25\,;\,\,31} \right)\] |
|
\[\]Tần số |
\(5\) |
\[10\] |
\[20\] |
\[15\] |
Mệnh đề sai là mệnh đề
Xem đáp án »
03/03/2025
793
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận