Cho đường tròn \(\left( {O;\,\,R} \right)\). Từ \(A\) trên \(\left( O \right),\) kẻ tiếp tuyến \(d\) với \(\left( O \right).\) Trên đường thẳng \(d\) lấy điểm \(M\) bất kỳ \(\left( M \right.\) khác \(\left. A \right),\) kẻ cát tuyến \(MNP.\) Gọi \(K\) là trung điểm của \(NP,\) kẻ tiếp tuyến \(MB\). Kẻ \[AC \bot MB,\,\,BD \bot AM\,\,\left( {C \in MB,\,\,D \in AM} \right).\] Gọi\[H\] là giao điểm của \[AC\] và \[BD,\] \[I\] là giao điểm của \[OM\] và \[AB.\]
a) Chứng minh tứ giác \(AMBO\) nội tiếp.
b) Chứng minh \(OI \cdot OM = {R^2}\) và \(OI \cdot IM = I{A^2}\).
c) Chứng minh ba điểm \(O,\,\,H,\,\,M\) thẳng hàng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
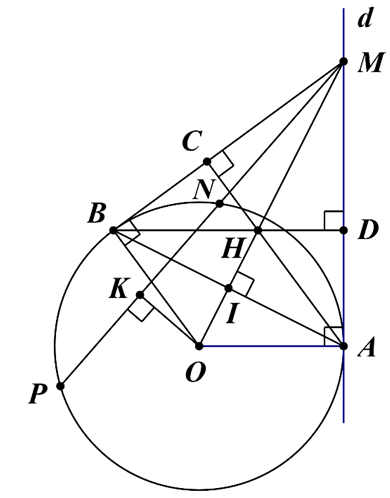
a) Ta có \(\widehat {OAM} = 90^\circ \) (do \[MA\] là tiếp tuyến của \[\left( O \right)\], \[A\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,A,\,\,M\) cùng thuộc một đường tròn đường kính \[OM. & \left( 1 \right)\]
Lại có \(\widehat {OBM} = 90^\circ \) (do \[MB\] là tiếp tuyến của \[\left( O \right)\], \[B\] là tiếp điểm).
Suy ra ba điểm \(O,\,\,B,\,\,M\) cùng thuộc một đường tròn đường kính \[OM. & \left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta được tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta được tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
b) Ta có tứ giác \[AMBO\] nội tiếp đường tròn đường kính \[OM.\]
Suy ra \[AB\] là dây cung của đường tròn đường kính \[OM.\]
Do đó \(OM \bot AB\).
Xét \(\Delta OAM\) vuông tại \[A\] có \[AI\] là đường cao.
Xét \(\Delta OAM\) và \[\Delta OIA\] là hai tam giác vuông có góc \[\widehat O\] chung nên
Suy ra \[\frac{{OA}}{{OI}} = \frac{{OM}}{{OA}}\] hay \[O{A^2} = OM.OI\] mà \[OA = R\] nên \(OI \cdot OM = {R^2}\).
Áp dụng định lí Pythagore trong tam giác vuông \[IOA\], ta có
\[I{A^2} = O{A^2} - O{I^2} = OI \cdot OM - O{I^2} = OI\left( {OM - OI} \right) = OI.IM\].
Ta có \(OA \bot AM\) (do \[AM\] là tiếp tuyến của \(\left( O \right)\) và \(BD \bot MA\) (gt), suy ra \[OA\,{\rm{//}}\,BD\].
Chứng minh tương tự, ta được \[OB\,{\rm{//}}\,{\rm{A}}C\].
Do đó tứ giác \[OAHB\] là hình bình hành.
Mà \(OA = OB = R\) nên tứ giác \[OAHB\] là hình thoi, suy ra \(OH \bot AB\).
Mà \(OM \bot AB\), do đó \[OM \equiv OH\].
Vậy ba điểm \[O,\,\,H,M\] thẳng hàng.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng.b) Đúng.c) Sai.d) Sai.
⦁ Thể tích hình nón có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \frac{1}{3}\pi {R^2}h.\)
Do đó ý a) là sai.
⦁ Chiều cao của phần rượu có trong ly là \[7 - 3 = 4\,\,\left( {{\rm{cm}}} \right)\]. Do đó ý b) là đúng.
⦁ Thể tích của cái ly thủy tinh là \[V = \frac{1}{3}\pi \cdot {4^2} \cdot 7 = \frac{{112}}{3}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right){\rm{.}}\] Do đó ý c) là sai.
⦁ Tỉ số giữa thể tích của phần còn lại trong ly rượu so với thể tích ly là: \[1 - {\left( {\frac{4}{7}} \right)^3} = \frac{{279}}{{343}}\].
Do đó ý d) là sai.
Lời giải
Hướng dẫn giải
Đáp số: 3.
Gọi \[x\] (xe) là số xe tải loại lớn cần sử dụng đề chở hết thiết bị \[\left( {x \in \mathbb{N}*} \right)\].
Số xe tải loại nhỏ cần sử dụng đề chở hết thiết bị là \[x + 2\] (xe).
Số tấn thiết bị mỗi xe tải loại lớn chở được là \(\frac{{15}}{x}\) (tấn).
Số tấn thiết bị mỗi xe tải loại nhỏ chở được là \(\frac{{15}}{{x + 2}}\) (tấn).
Theo bài ra ta có phương trình: \(\frac{{15}}{x} - \frac{{15}}{{x + 2}} = 2\)
\(15\left( {x + 2} \right) - 15x = 2x{\rm{\;}}\left( {{\rm{\;}}x + 2} \right)\)
\(15\left( {x + 2 - x} \right) = 2{x^2} + 4{\rm{\;}}x\)
\(2{x^2} + 4{\rm{\;}}x - 30 = 0\)
\({x^2} + 2{\rm{\;}}x - 15 = 0\)
\(x = 3\) (TMĐK) hoặc \[{\rm{\;}}x = - 5\] (loại)
Vậy đội vận chuyển sử dụng 3 xe tải loại lớn.
Câu 3
B. Tự luận
1. Kết quả nhảy xa của một lớp (đơn vị mét) được cho trong bảng sau:
|
2,4 |
3,1 |
2,7 |
2,8 |
3,2 |
2,8 |
4,1 |
3,2 |
|
2,1 |
3,2 |
2,1 |
3,2 |
2,3 |
2,5 |
2,6 |
3,3 |
|
3,6 |
2,0 |
2,0 |
2,7 |
3,1 |
2,3 |
4,3 |
3,9 |
|
3,9 |
3,5 |
3,6 |
3,7 |
2,7 |
3,5 |
3,5 |
2,4 |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số ghép nhóm hay tấn số không ghép nhóm? Vì sao?
b) Hãy lập bảng số liệu làm 5 nhóm trong đó nhóm cuối cùng cự li là từ 4,0 đến dưới 4,5 m. Lập bảng tần số và tần số tương đối ghép nhóm.
2. Cho hai túi I và II mỗi túi chứa 3 tấm thẻ được đánh số \[2\,;\,\,3\,;\,\,4.\] Rút ngẫu nhiên từ mỗi túi ra 1 tấm thẻ và ghép thành số có hai chữ số với chữ số trên tấm thẻ rút từ túi I là chữ số hàng chục. Tính xác suất của biến cố “Số tạo thành là số chia hết cho 3”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[m < - 2\].
B. \[m < 2\].
C. \[m > - 2\].
D. \[m > 2\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho bảng tần số ghép nhóm:
|
Nhóm |
\[\left[ {7\,;\,\,13} \right)\] |
\[\left[ {13\,;\,\,19} \right)\] |
\[\left[ {19\,;\,\,25} \right)\] |
\[\left[ {25\,;\,\,31} \right)\] |
|
\[\]Tần số |
\(5\) |
\[10\] |
\[20\] |
\[15\] |
Mệnh đề sai là mệnh đề
A. Tần số của nhóm là \[15\].
B. Tần số tương đối ghép nhóm của nhóm \[\left[ {7\,;\,\,13} \right)\] là \[10\% \].
C. Tần số tương đối ghép nhóm của nhóm \[\left[ {13\,;\,\,19} \right)\] là \[20\% \].
D. Tần số tương đối ghép nhóm của nhóm \[\left[ {19\,;\,\,25} \right)\] là \[30\% \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo