Câu hỏi:
03/03/2025 6,444Cho tam giác \[ABC\] nhọn có \[AB < AC\] nội tiếp đường tròn \[\left( {O;R} \right)\]. Các đường cao \[BE;\,\,CF\] của tam giác cắt nhau tại \[H\] \[\left( E \right.\] thuộc \[AC,\,\,F\]thuộc \[\left. {AB} \right).\]
a) Chứng minh: Tứ giác \[BFEC\] nội tiếp đường tròn.
b) Kẻ đường kính \[AK\] của đường tròn \[\left( O \right)\]. Chứng minh \[AK\] vuông góc với \[EF\].
c) Giả sử \[BC\] cố định và \[A\] di chuyển trên cung lớn \[BC\] sao cho tam giác\[ABC\] luôn là tam giác nhọn. Xác định vị trí của điểm \[A\] để diện tích tam giác \[EAH\] lớn nhất. Tính giá trị lớn nhất đó theo \[R\] khi \[BC = R\sqrt 3 .\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
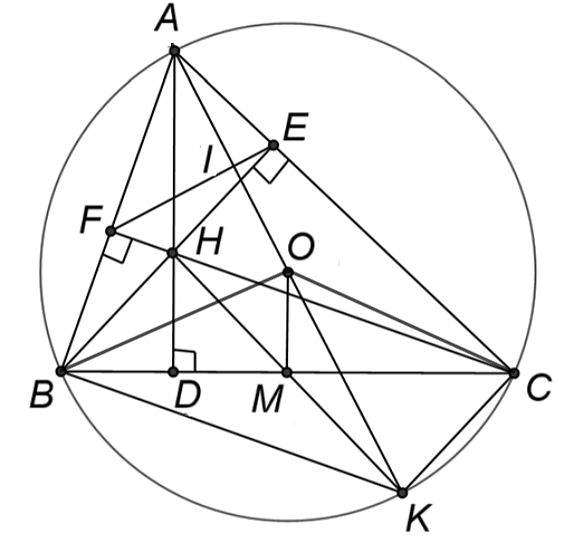
a) Ta có \[BE,\,\,CF\] là hai đường cao của tam giác \[ABC\] nên \[\widehat {BFC} = \widehat {BEC} = 90^\circ .\]
Tam giác \[BCE\] vuông tại \[E\] nên \[B,\,\,C,\,\,E\] thuộc đường tròn đường kính \[BC.\]
Tam giác \[BFC\] vuông tại \[F\] nên \[B,\,\,C,\,\,F\] thuộc đường tròn đường kính \[BC.\]
Do đó \[B,\,\,C,\,\,E,\,\,F\] thuộc đường tròn đường kính \[BC.\]
Hay tứ giác \[BFEC\] là tứ giác nội tiếp.
b) Vì tứ giác \[BFEC\] nội tiếp nên \[\widehat {AEF} = \widehat {ABC}\], mà \[\widehat {AKC} = \widehat {ABC}\] nên \[\widehat {AKC} = \widehat {AEF}.\]
Xét đường tròn \[\left( O \right)\] có \(\widehat {ACK} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên
\[\widehat {AKC} + \widehat {IAE} = 90^\circ \] hay \[\widehat {AEF} + \widehat {IAE} = 90^\circ .\]
Tam giác \[IAE\] vuông tại \[I\] nên \[AK \bot EF\] (đpcm).
c) Gọi \[M\] là giao điểm của \[BC\] và \[HK.\]
Vì \(\widehat {ABK},\,\,\widehat {ACK}\) đều là các góc nội tiếp chắn nửa đường tròn \[\left( O \right)\] nên \[\widehat {ABK} = 90^\circ ,\,\,\widehat {ACK} = 90^\circ \] hay \(AB \bot BK\,;\,\,AC \bot CK.\)
Vì \(AB \bot BK\) và \(AB \bot CF\) nên \[BK\,{\rm{//}}\,CF\] hay \[BK\,{\rm{//}}\,CH.\]
Vì \(AC \bot CK\) và \(AC \bot BE\) nên \[BE\,{\rm{//}}\,CK\] hay \[BH\,{\rm{//}}\,CK.\]
Xét tứ giác \(BHCK\) có \[BK\,{\rm{//}}\,CH\,;\,\,BH\,{\rm{//}}\,CK\] nên tứ giác \(BHCK\) là hình bình hành.
Suy ra hai đường chéo \(BC\) và \[HK\]cắt nhau tại trung điểm \[M\] của mỗi đường.
Xét tam giác \[AHK\] có \(O,\,\,M\) lần lượt là trung điểm của \(AK,\,\,HK\)
Suy ra \[OM\] là đường trung bình tam giác \[AHK\] nên \[AH = 2OM;\,\,OM\,{\rm{//}}\,AH.\]
Vì \[\Delta AEH\] vuông tại \[E\] nên \({S_{AEH}} = \frac{1}{2}AE \cdot EH \le \frac{1}{2} \cdot \frac{{A{E^2} + E{H^2}}}{2} = \frac{{A{H^2}}}{4} = O{M^2}. & \left( 1 \right)\)
Vì \[M\] là trung điểm của \(BC\) nên \[BM = \frac{{BC}}{2} = \frac{{R\sqrt 3 }}{2}.\]
Vì \[OM\,{\rm{//}}\,AH\] và \(AH \bot BC\) nên \(OM \bot BC.\)
Áp dụng định lí Pythagore vào \(\Delta OBM\) vuông tại \(M\) \(\left( {OM \bot BC} \right)\), ta có: \(O{B^2} = O{M^2} + B{M^2}\)
Khi đó \[O{M^2} = O{B^2} - B{M^2} = {R^2} - {\left( {\frac{{R\sqrt 3 }}{2}} \right)^2} = {R^2} - \frac{3}{4}{R^2} = \frac{{{R^2}}}{4}.\] Suy ra \(OM = \frac{R}{2}. & \left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \({S_{AEH}} \le \frac{{{R^2}}}{4}\).
Dấu xảy ra khi \[AE = EH\] nên \(\widehat {EAH} = 45^\circ \) hay \(\widehat {ACB} = 45^\circ \).
Vậy \[{\left( {{S_{AEH}}} \right)_{\max }} = \frac{{{R^2}}}{4}\] khi \[A\] thuộc cung lớn \[BC\] và \[\widehat {ACB} = 45^\circ .\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 30.
Gọi vận tốc của xe tải là \(x\,\,({\rm{km/h}})\,\,\,\left( {x > 0} \right).\)
Khi đó, vận tốc của xe khách là \(x\, + \,10\,\,({\rm{km/h}}).\)
Thời gian đi hết quãng đường của xe tải là \(\frac{{132}}{x}\) (giờ) và của xe khách là \(\frac{{132}}{{x + 10}}\) (giờ).
Đổi 1 giờ 6 phút \( = \,\frac{{11}}{{10}}\) giờ.
Vì xe khách đi nhanh hơn xe tải 1 giờ 6 phút nên ta có phương trình:
\(\frac{{132}}{x} - \frac{{132}}{{x + 10}} = \frac{{11}}{{10}}\)
\(\frac{{12}}{x} - \frac{{12}}{{x + 10}} = \frac{1}{{10}}\)
\(120\left( {x + 10} \right) - 120x = x\left( {x + 10} \right)\)
\(120x + 1200 - 120x = {x^2} + 10x\)
\[{x^2} + 10x - 1200 = 0\]
\(x = 30\) (TMĐK) hoặc \[{\rm{\;}}x = - 40\] (loại).
Vậy vận tốc của xe tải là \(30\,\,{\rm{km/h}}{\rm{.}}\)
Lời giải
Hướng dẫn giải
Đáp số: \(0,4\).
Kí hiệu ba bóng đỏ lần lượt là \[{D_1};\,\,{D_2};\,\,{D_3}\] và hai bóng vàng lần lượt là \[{V_1};\,\,{V_2}\].
Khi đó không gian mẫu là:
\[\Omega = \left\{ {\left( {{D_1};{D_2}} \right);\,\,\left( {{D_1};{D_3}} \right);\,\,\left( {{D_2};{D_3}} \right);\,\,\left( {{V_1};{V_2}} \right);\left( {{D_1};{V_1}} \right);\left( {{D_1};{V_2}} \right);\left( {{D_2};{V_1}} \right);\left( {{D_2};{V_2}} \right);\left( {{D_3};{V_1}} \right);\,\,\left( {{D_3};{V_2}} \right)} \right\}.\]
Do đó, không gian mẫu có 10 phần tử.
Gọi \[A\] là biến cố “Hai bóng lấy ra cùng màu”.
Khi đó, các kết quả thuận lợi của biến cố \[A\] là \[\left\{ {\left( {{D_1};{D_2}} \right);\,\,\left( {{D_1};{D_3}} \right);\,\,\left( {{D_2};\,{D_3}} \right);\,\,\left( {{V_1};\,\,{V_2}} \right)} \right\}\] nên có 4 kết quả thuận lợi cho biến cố \[A\].
Do đó, xác suất để hai quả bóng lấy ra cùng màu \(P\left( A \right) = \frac{4}{{10}} = \frac{2}{5}\).
Vậy xác suất để hai bóng lấy ra cùng màu là \(0,4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo