Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáy là \[4,4{\rm{ cm,}}\] chiều cao vỏ quế \[12{\rm{ cm}}\,{\rm{.}}\] Người ta lấy phần kem từ một hộp hình trụ có chiều cao là \[15{\rm{ cm}}\] với diện tích đáy \(100\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\) để cho vào vỏ ốc quế (coi phần vỏ kem có độ dày không đáng kể).

a) Thể tích hình trụ có bán kính đáy \(R\) và chiều cao \(h\), được tính bằng công thức: \(V = \frac{1}{3}\pi {R^2}h.\)

b) Bán kính đáy của chiếc kem ốc quế là \(R = 2,2\,\,{\rm{cm}}\,{\rm{.}}\)

c) Thể tích của chiếc kem là \(\frac{{1452}}{{25}}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)

d) Ta có thể lấy kem từ hộp làm được tối đa 75 chiếc kem ốc quế.

Hướng dẫn giải

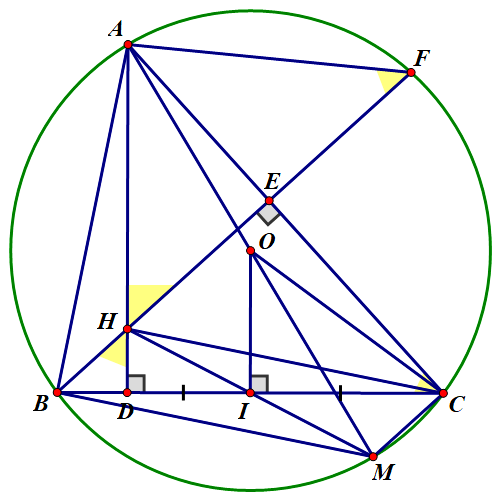
a) Gọi \(O'\) là trung điểm của cạnh \[CH.\]

Ta có \(HD \bot CD\) nên \(\widehat {HDC} = 90^\circ \).

Xét \(\Delta HDC\)vuông tại \[D\] có \(DO'\) là trung tuyến nên \(DO' = HO' = CO' = \frac{1}{2}HC\).

Chứng ming tương tự, ta có \(CO' = HO' = EO' = \frac{1}{2}HC\).

Do đó \(DO' = HO' = CO' = EO' = \frac{1}{2}HC\).

Vậy bốn điểm \(D,\,\,H,\,\,E,\,\,C\) cùng thuộc một đường tròn.

Vậy tứ giác \(DHEC\) nội tiếp đường tròn.

b) Trong tam giác \(ABC\) có \(BE,\,\,AD\) là hai đường cao cắt nhau tại \(H\).

Vì \(H\) là trực tâm tam giác \(ABC\) nên \(CH \bot AB\).

Trong\(\left( O \right)\) có \(\widehat {ABM},\,\,\widehat {ACM}\) là hai góc nội tiếp cùng chắn nửa đường tròn đường kính \(AM\).

Suy ra \(\widehat {ABM} = \widehat {ACM} = 90^\circ \) nên \(MB \bot AB\,;\,\,MC \bot AC.\)

Mà \(CH \bot AB\,;\,\,BH \bot AC\) nên \(MB\,{\rm{//}}\,CH,\,\,MC\,{\rm{//}}\,BH\) nên \(BHCM\) là hình bình hành.

Xét đường tròn \(\left( O \right)\) có \(OI \bot BC\) tại \(I\) nên \(I\) là trung điểm của \(BC\) (đường kính vuông góc với dây).

c) Xét \(\Delta DHB\) và \(\Delta DCA\) có

\(\widehat {BDH} = \widehat {ADC} = 90^\circ \) (vì \(AD \bot BC\))

\(\widehat {HBD} = \widehat {DAC}\) (cùng phụ \(\widehat {ACB}\))

Do đó .

Suy ra \(\frac{{DH}}{{DC}} = \frac{{DB}}{{DA}}\) hay \(DH \cdot DA = DB \cdot DC.\)

Ta có \({\left( {a - b} \right)^2} \ge 0\) hay \({a^2} - 2ab + {b^2} \ge 0\) nên \({a^2} + 2ab + {b^2} \ge 4ab\), suy ra \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\).

Áp dụng bất đẳng thức \(ab \le \frac{{{{\left( {a + b} \right)}^2}}}{4}\), ta có: \(DB \cdot DC \le \frac{{{{\left( {DB + DC} \right)}^2}}}{4} = \frac{{B{C^2}}}{4}\).

Suy ra \(DH \cdot DA \le \frac{{B{C^2}}}{4}\) không đổi vì \(BC\) cố định.

Dấu xảy ra khi \(DB = DC\), khi đó \(A\) là điểm chính giữa cung lớn .

Vậy \(A\) là điểm chính giữa cung lớn thì giá trị lớn nhất của \(DH \cdot DA\) bằng \(\frac{{B{C^2}}}{4}\).

Hướng dẫn giải

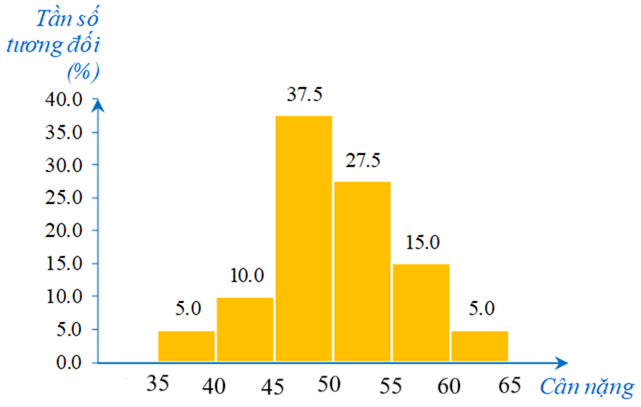
1. a) Từ biểu đồ trên, ta có bảng tần số ghép nhóm tương ứng như sau:

b) Bạn lớp trưởng cho rằng có trên 50% số học sinh của lớp có cân nặng từ 50 kg trở lên. Nhận định đó đúng hay sai? Tại sao?

Vì có có 11 học sinh có cân nặng từ 50 kg đến dưới 55 kg. nên số học sinh của lớp đó là:

11 : 27,5% = 40 (học sinh).

Số học sinh từ [56; 60) là \(40 \cdot 15\% = 6\) (học sinh).

Số học sinh [60; 66) là \(40 \cdot 5\% = 2\) (học sinh).

Tổng số học sinh từ 50 kg trở lên là (học sinh).

Vậy nhận định đó là sai.

2. Không gian mẫu của phép thử là \[\Omega = \left\{ {1\,;\,\,2\,;\,\,3\,;\,\, \ldots \,;\,\,52} \right\}\].

Do đó \[n\left( \Omega \right) = 52\].

Gọi \[B\] là biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1”.

Ta có \[B = \left\{ {1\,;\,\,21\,;\,\,41} \right\}\] nên \[n\left( B \right) = 3\].

Xác suất của biến cố \[B\] là \[P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{3}{{52}}\].