Bảng thống kê sau cho biết số lượt mượn các loại sách trong một tuần tại thư viện của một trường Trung học cơ sở như sau:
Loại sách | Sách giáo khoa | Sách tham khảo | Truyện ngắn | Tiểu thuyết |
Số lượt | 20 | 80 | 70 | 30 |
Từ bảng thống kê, tần số tương đối về số lượng sách giáo khoa được mượn là
A. \(10{\rm{\% }}\)
B. \(15{\rm{\% }}\).
C. \(35{\rm{\% }}\).
D. \[40{\rm{\% }}.\].
Quảng cáo
Trả lời:
Đáp án đúng là: A
Tần số tương đối về số lượng sách giáo khoa được mượn là:
\(\frac{{20}}{{20 + 80 + 70 + 30}} = \frac{{20}}{{200}} = 0,1 = 10\% \).
Do đó ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng.b) Sai.c) Đúng.d) Sai.
⦁ Thể tích hình cầu có bán kính đáy \(R\), được tính bằng công thức: \(V = \frac{4}{3}\pi {R^3}.\)
Do đó ý a) là đúng.
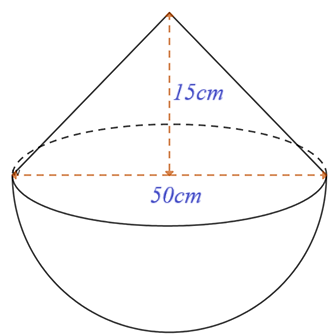
⦁ Phần gạo nằm ngang mặt thúng trở xuống có dạng nửa hình cầu có bán kính \[\frac{{50}}{2} = 25\,\,\left( {{\rm{cm}}} \right).\] Do đó ý b) là sai.
⦁ Phần gạo nằm ngang mặt thúng trở xuống có dạng nửa hình cầu có bán kính \(25\,\,{\rm{cm}}\) có thể tích là \({V_1} = \frac{1}{2} \cdot \frac{4}{3}\pi \cdot {25^3} = \frac{{31\,\,250}}{3}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Phần gạo nằm trên miệng thúng có dạng hình nón có chiều cao \(15cm\) và bán kính đáy \(\frac{{50}}{2} = 25\,\,\left( {{\rm{cm}}} \right)\) có thể tích là \({V_2} = \frac{1}{3} \cdot 15 \cdot \pi \cdot {25^2} = 3\,\,125\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Khi đó thể tích gạo trong thúng là \(V = {V_1} + {V_2} = \frac{{31\,\,250}}{3}\pi + 3\,\,125\pi = \frac{{60\,\,625}}{3}\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Do đó ý c) là đúng.
⦁ Thể tích lon là \(V = \pi \cdot {5^2} \cdot 15 = 375\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\).
Vì lượng gạo chiếm \[90\% \] thể tích lon nên thể tích gạo trong mỗi lần lấy là:
\(375\pi \cdot 90\% = 337,5\pi \,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right).\)
Khi đó mỗi ngày nhà Danh ăn hết số gạo có thể tích là: \(337,5\pi \cdot 5 = 1687,5\pi \,\,\left( {c{m^3}} \right).\)
Vậy với số gạo ở thúng trên thì nhà Danh ăn được số ngày là: \(\frac{{\frac{{60\,\,625}}{3}\pi }}{{1687,5\pi }} \approx 12\) (ngày).
Do đó ý d) là sai.
Lời giải
Hướng dẫn giải
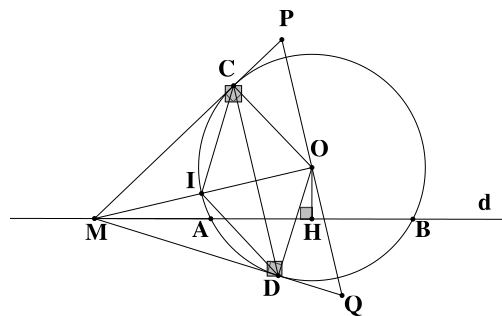
a) Vì \(MC,\,\,MD\) là tiếp tuyến của \(\left( {O\,;\,\,R} \right)\) \(\left( {C,\,\,\,D} \right.\) là hai tiếp điểm) nên \(MC \bot OC,\,\)\(\,MD \bot OD.\)
Suy ra \(\widehat {OCM} = \widehat {ODM} = 90^\circ \) nên \(C,\,\,D\) thuộc đường tròn đường kính \(OM\).
Vì \(H\) là trung điểm của \(AB\) và \(AB\) là dây của \(\left( {O\,;\,\,R} \right)\) nên \(OH \bot AB\).
Suy ra \(\widehat {OHM} = 90^\circ \) nên \(H\) thuộc đường tròn đường kính \(OM\).
Vậy \(M,\,\,D,\,\,O,\,\,H\) cùng nằm trên đường tròn đường kính \(OM\).
b) Vì \(MC,\,\,MD\) là tiếp tuyến của \(\left( {O\,;\,\,R} \right)\)\(\left( {C,\,\,\,D} \right.\) là hai tiếp điểm) nên \(MO\) là tia phân giác của \(\widehat {CMD}\) và \(OM\) là tia phân giác của \(\widehat {COD}.\)
Mặt khác, \(\widehat {MCI} = \widehat {CDI}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn ).
và \(\widehat {CDI} = \widehat {DCI}\) (tam giác \(CDI\) cân tại \[I\,)\].
Suy ra \[\widehat {MCI} = \widehat {DCI}\] nên \[CI\] là tia phân giác của \(\widehat {MCD}\).
Ta có \(I\) là giao điểm hai đường phân giác trong của tam giác \(MCD\) nên \(I\) là tâm đường tròn nội tiếp tam giác \(MCD.\)
c) Ta có \({S_{MPQ}} = 2{S_{MPO}} = MP \cdot OC = \left( {MC + CP} \right) \cdot R\).
Mà \(MC + CP \ge 2\sqrt {MC.CP} = 2\sqrt {O{C^2}} = 2R\) nên \({S_{MPQ}} \ge 2{R^2}\).
Dấu xảy ra khi \(MC = CP = R\) hay \(OM = R\sqrt 2 \).
Vậy để diện tích tam giác \(MPQ\) nhỏ nhất thì \(M\) là giao điểm của \(\left( {O\,;\,\,R\sqrt 2 } \right)\) và đường thẳng \(d.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
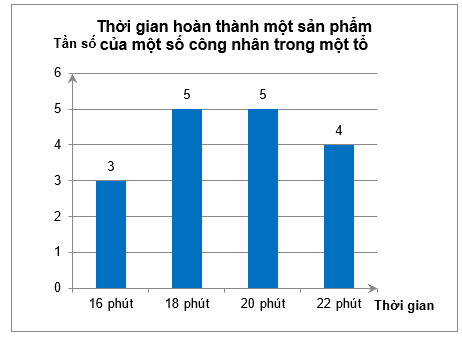
A. 5 phút.
B. 17 phút.
C. 18 phút và 20 phút.
D. 20 phút và 22 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
B. Tự luận
1. Bạn Hoa được cô yêu cầu ghi lại thời gian chạy 1000 m của các bạn trong lớp (đơn vị: giây):
|
\[4:08\] |
\[4:00\] |
\[4:16\] |
\[4:12\] |
\[5:11\] |
\[4:52\] |
\[4:12\] |
\[4:30\] |
\[4:37\] |
|
\[5:12\] |
\[5:00\] |
\[5:17\] |
\[5:14\] |
\[4:13\] |
\[4:22\] |
\[4:02\] |
\[4:05\] |
\[5:42\] |
|
\[4:39\] |
\[5:32\] |
\[5:11\] |
\[4:40\] |
\[4:05\] |
\[5:02\] |
\[4:27\] |
\[4:50\] |
\[4:23\] |
|
\[5:48\] |
\[5:22\] |
\[4:37\] |
\[4:23\] |
\[5:00\] |
\[5:18\] |
\[5:17\] |
\[4:49\] |
\[5:12\] |
a) Để thu gọn bảng dữ liệu trên thì nên chọn bảng tần số không ghép nhóm hay tần số ghép nhóm để biểu thị dữ liệu? Tại sao?
b) Hãy chia số liệu làm 4 nhóm trong đó nhóm đầu tiên là \[4:00\] đến dưới \[4:30\]; lập bảng tần số và tần số tương đối ghép nhóm (làm tròn đến hàng đơn vị).
2. Viết ngẫu nhiên một số tự nhiên có hai chữ số nhỏ hơn 100.
Tính xác suất của mỗi biến cố \[A:\] “Số tự nhiên được viết ra là số tròn chục”.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.