Câu hỏi trong đề:
10000 câu trắc nghiệm tổng hợp môn Toán 2025 mới nhất (có đáp án) !!
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử chứng minh Oz nằm giữa Oy và Ox
- Cách 1: cho 3 tia Ox, Oy, Oz chung gốc. Lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy (A,B ≠ O). Nếu đoạn AB cắt tia Oz tại một điểm bất kì thì Oz nằm giữa 2 tia Ox, Oy.
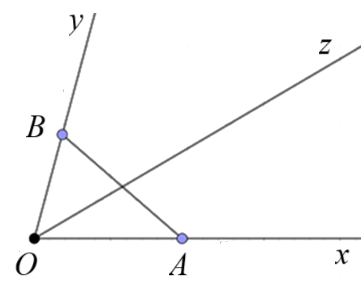
- Cách 2: cho 2 tia Ox, Oy đối nhau. Bất kì điểm nào chung gốc O đều nằm giữa 2 tia Ox, Oy.
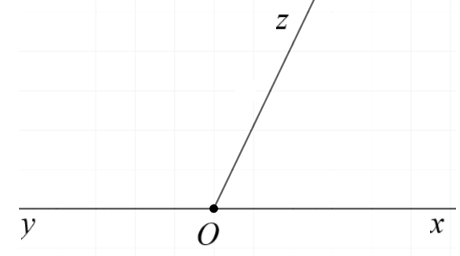
- Cách 3: Cho 2 tia Oy, Oz thuộc cùng nửa mặt phẳng bờ chứa tia Ox. Mà \(\widehat {xOz} < \widehat {xOy}\) suy ra tia Oz nằm giữa 2 tia Ox, Oy.
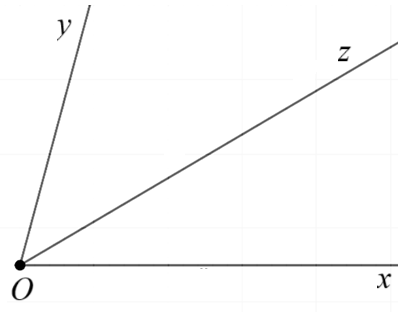
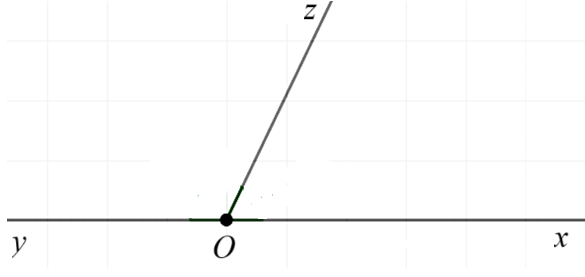
- Cách 4: Lấy hai tia Ox, Oy thuộc 2 nửa mặt phẳng đối nhau bờ là đường thẳng chứa tia Oz. Mà \(\widehat {xOz} + \widehat {xOy}\) ≤ 180° suy ra tia Oz nằm giữa 2 tia Ox và Oy.
- Cách 5: Nếu \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\) suy ra tia Oz nằm giữa 2 tia Ox, Oy.
Nhà sách VIETJACK:
Combo - Sách 20 Bộ đề, Tổng ôn, sổ tay ôn thi 2025 môn Toán (3 quyển) - Mới nhất cho 2k7
Đã bán 386
₫ 110.000
₫ 55.000
Sách - 20 đề thi tốt nghiệp môn Toán (Sách dành cho ôn thi THPT Quốc gia 2025) VietJack
Đã bán 189
₫ 135.000
₫ 38.500
Combo - Sổ tay Lý thuyết trọng tâm lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL
Đã bán 1,5k
₫ 70.000
₫ 36.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 6:
Số tập con có 3 phần tử của tập {21;22;...;22020} sao cho ba phần tử đó có thể xếp thành 1 cấp số nhân tăng bằng?
Số tập con có 3 phần tử của tập {21;22;...;22020} sao cho ba phần tử đó có thể xếp thành 1 cấp số nhân tăng bằng?
Xem đáp án »
13/03/2025
413
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận