Câu hỏi:
17/03/2025 100
(1,5 điểm) Cho tam giác \[ABC{\rm{ }}\left( {AB < AC} \right)\] vuông tại \[A\] có đường cao \[AH.\]
a) Chứng minh rằng
(1,5 điểm) Cho tam giác \[ABC{\rm{ }}\left( {AB < AC} \right)\] vuông tại \[A\] có đường cao \[AH.\]
a) Chứng minh rằng
Câu hỏi trong đề:
Bộ 5 đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 49k/cuốn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét \(\Delta ABC\) và \(\Delta HAC\), có: \(\widehat {BAC} = \widehat {AHC} = 90^\circ \) (gt) và \(\widehat {ACB} = \widehat {HCA}\) (gt)
Do đó, (g.g)
Câu hỏi cùng đoạn
Câu 2:
b) Lấy điểm \(I\) thuộc đoạn \(AH\) (\(I\)không trùng với \[A,H\]). Qua \[B\] kẻ đường thẳng vuông góc với \[CI\] tại \[K\]. Chứng minh rằng \[CH.CB = CI.CK.\]
b) Lấy điểm \(I\) thuộc đoạn \(AH\) (\(I\)không trùng với \[A,H\]). Qua \[B\] kẻ đường thẳng vuông góc với \[CI\] tại \[K\]. Chứng minh rằng \[CH.CB = CI.CK.\]
Lời giải của GV VietJack
Xét \(\Delta CHI\) và \(\Delta CKB\), ta có:
\(\widehat {CHI} = \widehat {CKB} = 90^\circ \) (gt)
\(\widehat {HCI} = \widehat {KCB}\)
Do đó, (g.g)
Suy ra \(\frac{{CH}}{{CK}} = \frac{{CI}}{{CB}}\).
Suy ra \(CH.CB = CI.CK\).
Câu 3:
c) Tia \[BK\] cắt tia \[HA\] tại điểm \[D.\] Chứng minh \[CH.CB + DK.DB = C{D^2}.\]
c) Tia \[BK\] cắt tia \[HA\] tại điểm \[D.\] Chứng minh \[CH.CB + DK.DB = C{D^2}.\]
Lời giải của GV VietJack
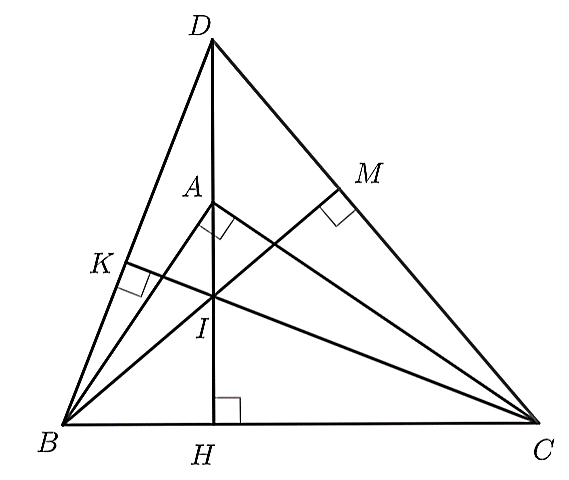
Gọi \(M\) là giao điểm của \(BI\) và \(DC\). Vì \(I\) là trực tâm của \(\Delta BDC\) nên \(BI \bot DC\).
Xét \(\Delta CMI\) và \(\Delta CDK\), ta có: \(\widehat {CMI} = \widehat {CKD} = 90^\circ \) (gt) và \(\widehat {MCI} = \widehat {DCK}\) (gt)
Suy ra (g.g)
Suy ra \(\frac{{CM}}{{CK}} = \frac{{CI}}{{CD}}\) nên \(CD.CM = CI.CK\).
Mà từ phần b) ta có: \(CH.CB = CI.CK\) suy ra \(CH.CB = CI.CK = CD.CM.\)
Chứng minh được (g.g) suy ra \(DK.DB = DM.DC\).
Do đó, \(CH.CB + DK.DB = CM.CD + DM.DC = DC\left( {MD + MC} \right) = D{C^2}\).
Nhà sách VIETJACK:
Sách - Sổ tay Toán 8 (Takenote) cho cả 3 bộ Kết nối tri thức, Chân trời sáng tạo, Cánh diều VietJack
Đã bán 212
₫ 60.000
₫ 30.000
Trọng tâm Văn - Sử - Địa - GDCD lớp 8 dùng cả 3 sách Kết nối, Cánh diều, Chân trời VietJack - Sách 2025
Đã bán 123
₫ 130.000
₫ 60.000
Combo 2 sách Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 cho cả 3 bộ KNTT; CTST; CD VietJack
Đã bán 287
₫ 230.000
₫ 120.000
Combo 2 sách Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 cho cả 3 bộ KNTT; CTST; CD VietJack
Đã bán 361
₫ 245.000
₫ 126.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Có \(20\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”.
a) Có \(20\) kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số lẻ”.
Xem đáp án »
17/03/2025
237
Câu 2:
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Đường thẳng \(y = 1\) luôn cắt trục tung tại điểm
A. TRẮC NGHIỆM (7,0 điểm)
Phần 1. (3,0 điểm) Câu trắc nghiệm nhiều phương án lựa chọn
Trong mỗi câu hỏi từ câu 1 đến câu 12, hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất vào bài làm.
Đường thẳng \(y = 1\) luôn cắt trục tung tại điểm
Xem đáp án »
17/03/2025
207
Câu 3:
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {0;5} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Xác định hệ số góc của đường thẳng đi qua hai điểm \(A\left( { - 4;0} \right)\) và \(B\left( {0;5} \right)\).
(Kết quả ghi dưới dạng số thập phân)
Xem đáp án »
17/03/2025
188
Câu 6:
Cho các hình vẽ sau:
Đoạn thẳng \(MN\) là đường trung bình của tam giác \(ABC\) trong hình vẽ nào?
Cho các hình vẽ sau:
Xem đáp án »
17/03/2025
144
Câu 7:
Cho hình vẽ dưới đây:
Hệ thức theo Định lí Thalès của hình trên là
Xem đáp án »
17/03/2025
125
🔥 Đề thi HOT:
-
Đề kiểm tra Cuối kì 1 Toán 8 KNTT có đáp án (Đề 1)
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 1)
-
10 Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore (có lời giải)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 5 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
-
10 Bài tập Bài toán thực tiễn gắn với việc vận dụng định lí Thalès (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận