(1,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB < AC} \right)\), đường cao \(AH\) \(\left( {H \in BC} \right)\).
a) Chứng minh và \(AB.AH = AC.HB.\)
(1,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB < AC} \right)\), đường cao \(AH\) \(\left( {H \in BC} \right)\).
a) Chứng minh và \(AB.AH = AC.HB.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
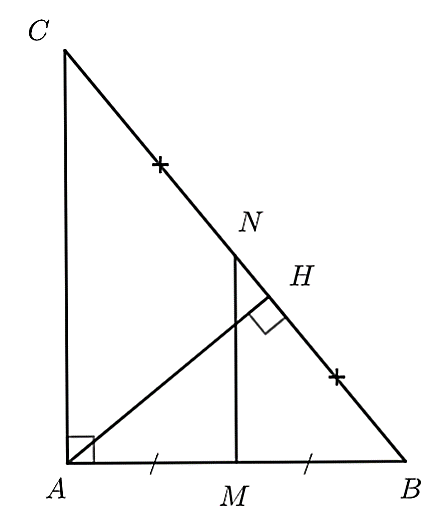
Xét \(\Delta ABC\) và \(\Delta BHA\) có: \(\widehat {BAC} = \widehat {BHA} = 90^\circ \) (gt); \(\widehat {CBA}\) chung (gt)
Suy ra (g.g)
Do đó, \(\frac{{AB}}{{HB}} = \frac{{AC}}{{HA}}\) nên \(AB.AH = AC.HB\) (đpcm).
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh rằng \(A{H^2} = BH.CH.\)
b) Chứng minh rằng \(A{H^2} = BH.CH.\)
Lời giải của GV VietJack
Vì (cmt) suy ra \(\widehat {ACB} = \widehat {HAB}\) (hai góc tương ứng)
Xét \(\Delta BHA\) và \(\Delta CHA\), có:
\(\widehat {HAB} = \widehat {HCA}\) (cmt) và \(\widehat {AHB} = \widehat {CHA} = 90^\circ \) (gt)
Suy ra (g.g)
Suy ra \(\frac{{AH}}{{CH}} = \frac{{HB}}{{HA}}\) hay \(A{H^2} = BH.CH\).
Câu 3:
c) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(BC.\) Chứng minh: \(\frac{1}{4}CH.CB = M{N^2}.\)
c) Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(BC.\) Chứng minh: \(\frac{1}{4}CH.CB = M{N^2}.\)
Lời giải của GV VietJack
Có \(M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(BC\) nên \(MN\) là đường trung bình của \(\Delta ABC\).
Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat {CAB} = \widehat {AHC} = 90^\circ \) (gt)
\(\widehat {ACB}\) chung (gt)
Do đó, (g.g)
Suy ra \(\frac{{AC}}{{CH}} = \frac{{CB}}{{CA}}\) hay \(A{C^2} = CH.CB\).
Lại có \(MN\) là đường trung bình của \(\Delta ABC\) nên \(MN = \frac{1}{2}AC\) hay \(AC = 2MN\).
Suy ra \(4M{N^2} = CH.CB\) hay \(\frac{1}{4}CH.CB = M{N^2}\) (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(9,9\)
Tổng lượng tinh bột sắn mà các thị trường cung cấp cho Đài Loan trong 9 tháng năm 2022 là
\(218{\rm{ }}155 + 24{\rm{ }}859 + 3{\rm{ }}447 + 2{\rm{ }}983 + 483 = 249{\rm{ }}927\) (tấn)
Thị trường Việt Nam cung cấp lượng tinh bột sắn cho Đài Loan trong 9 tháng năm 2022 chiếm số phần trăm so với tổng lượng tinh bột sẵn mà các thị trường cung cấp cho Đài Loan trong 9 tháng năm 2022 là: \(\frac{{24{\rm{ }}859}}{{249{\rm{ }}927}}.100\% \approx 9,9\% \)
Lời giải
\(\frac{{2027 - x}}{{73}} + \frac{{2025 - x}}{{75}} + \frac{{2023 - x}}{{77}} + \frac{{2021 - x}}{{79}} + 4 = 0\)
\(\left( {\frac{{2027 - x}}{{73}} + 1} \right) + \left( {\frac{{2025 - x}}{{75}} + 1} \right) + \left( {\frac{{2023 - x}}{{77}} + 1} \right) + \left( {\frac{{2021 - x}}{{79}} + 1} \right) = 0\)
\(\frac{{2100 - x}}{{73}} + \frac{{2100 - x}}{{75}} + \frac{{2100 - x}}{{77}} + \frac{{2100 - x}}{{79}} = 0\)
\(\left( {2100 - x} \right)\left( {\frac{1}{{73}} + \frac{1}{{75}} + \frac{1}{{77}} + \frac{1}{{79}}} \right) = 0\)
Vì \(\frac{1}{{73}} + \frac{1}{{75}} + \frac{1}{{77}} + \frac{1}{{79}} \ne 0\) nên \(2100 - x = 0\), suy ra \(x = 2100\).
Vậy nghiệm của phương trình là \(x = 2100\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo