Một hòn đảo nằm trong một hồ nước. Biết rằng đường cong tạo nên hòn đảo được mô hình hóa vào hệ trục tọa độ 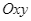 là một phần của đồ thị hàm số bậc ba
là một phần của đồ thị hàm số bậc ba 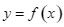 như hình vẽ.
như hình vẽ.
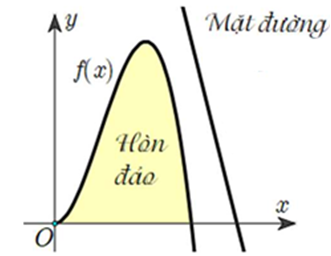
Vị trí điểm cực đại là 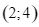 với đơn vị của hệ trục là 100 m và vị trí điểm cực tiểu là gốc tọa độ
với đơn vị của hệ trục là 100 m và vị trí điểm cực tiểu là gốc tọa độ 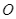 . Mặt đường chạy trên một đường thẳng có phương trình
. Mặt đường chạy trên một đường thẳng có phương trình 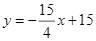 . Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét (nhập đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị).
. Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét (nhập đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị).
Đáp án: _______
Một hòn đảo nằm trong một hồ nước. Biết rằng đường cong tạo nên hòn đảo được mô hình hóa vào hệ trục tọa độ ![]() là một phần của đồ thị hàm số bậc ba
là một phần của đồ thị hàm số bậc ba ![]() như hình vẽ.
như hình vẽ.

Vị trí điểm cực đại là ![]() với đơn vị của hệ trục là 100 m và vị trí điểm cực tiểu là gốc tọa độ
với đơn vị của hệ trục là 100 m và vị trí điểm cực tiểu là gốc tọa độ ![]() . Mặt đường chạy trên một đường thẳng có phương trình
. Mặt đường chạy trên một đường thẳng có phương trình ![]() . Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét (nhập đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị).
. Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét (nhập đáp án vào ô trống, kết quả làm tròn đến hàng đơn vị).
Đáp án: _______
Quảng cáo
Trả lời:
Đáp án đúng là "64"
Phương pháp giải
Phương trình tiếp tuyến của đồ thị hàm số ![]() tại điểm có hoành độ
tại điểm có hoành độ ![]() là:
là:
![]()
Lời giải
Đồ thị hàm số bậc ba ![]() có điểm cực đại
có điểm cực đại ![]() và điểm cực tiểu là
và điểm cực tiểu là ![]() nên
nên ![]() .
.
Ta có: ![]()
Gọi ![]() là điểm nằm trên
là điểm nằm trên ![]() được chọn làm vị trí bắc cầu. Để cầu có độ dài ngắn nhất thì tiếp tuyến
được chọn làm vị trí bắc cầu. Để cầu có độ dài ngắn nhất thì tiếp tuyến ![]() của
của ![]() tại
tại ![]() phải song song với đường thẳng
phải song song với đường thẳng ![]() .
.
Phương trình tiếp tuyến ![]() của
của ![]() tại
tại ![]() :
: ![]()
Điều kiện cần để ![]() và
và ![]() song song là
song song là
![]() . Do đó
. Do đó ![]() .
.
Phương trình đường thẳng ![]() là:
là: ![]() . Kiểm tra, thấy
. Kiểm tra, thấy ![]() .
.
Khi đó, khoảng cách từ ![]() đến đường thẳng
đến đường thẳng ![]() là
là 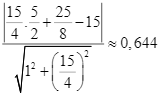
Vậy độ dài ngắn nhất của cây cầu là ![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là A
Phương pháp giải
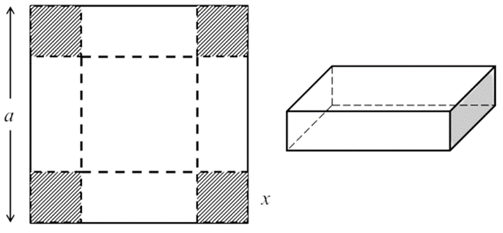
Lập hàm số thể tích cái hộp không nắp theo biến ![]() , sau đó tìm giá trị lớn nhất của hàm số vừa lập.
, sau đó tìm giá trị lớn nhất của hàm số vừa lập.
Lời giải
Cạnh đáy của cái hộp không nắp là ![]() . Điều kiện:
. Điều kiện: ![]() .
.
Thể tích của cái hộp không nắp là ![]()
Xét hàm số ![]() trên
trên ![]()
![]() liên tục trên
liên tục trên ![]()
![]()
![]() (loại)
(loại)
BBT
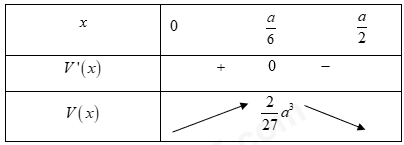
Dựa vào 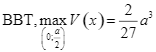 đạt tại
đạt tại ![]() . Khi đó, cạnh đáy của cái hộp là
. Khi đó, cạnh đáy của cái hộp là ![]() .
.
Lời giải
Đáp án đúng là B
Phương pháp giải
Công thức Bayes: 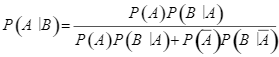 .
.
Lời giải
Gọi ![]() là biến cố "người được chọn nghiện thuốc lá".
là biến cố "người được chọn nghiện thuốc lá".
Gọi ![]() là biến cố "người được chọn bị bệnh phổi".
là biến cố "người được chọn bị bệnh phổi".
Ta cần tính ![]() .
.
Ta có: ![]() .
.
Theo công thức Bayes, ta có
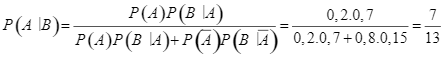
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. tháng 2 năm 2023.
C. tháng 4 năm 2023.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. tồn tại dưới dạng cation và di chuyển về cực âm (−) nguồn điện.
B. tồn tại dưới dạng anion và di chuyển về cực dương (+) nguồn điện.
C. tồn tại dưới dạng anion và di chuyển về cực âm (−) nguồn điện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 0,31(s)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.