Câu hỏi:

12/03/2026 676

Cho $\Delta ABC$ vuông tại $C$ có $\widehat A = 60^\circ .$ Trên cạnh $AB$ lấy điểm $K$ sao cho $AK = AC$. Từ $K$ kẻ đường thẳng vuông góc với $AB$, cắt $BC$ tại $E.$

a) $\Delta ACE = \Delta AEK$.

Xem lời giải

Câu hỏi trong đề: Bộ 5 Đề thi cuối kì 2 Toán 7 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Sai

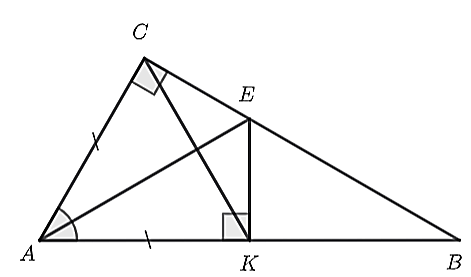
$a) $\Delta ACE = \Delta AEK$. (ảnh 1)$

Xét $\Delta ACE$ và $\Delta AEK$, ta có:

$\widehat {ACE} = \widehat {AKE} = 90^\circ $ (gt)

$CA = AK$ (gt)

$AE$ chung (gt)

Do đó, $\Delta ACE = \Delta AKE$ (ch – cgv)

Câu hỏi cùng đoạn

Câu 2:

b) $AE$ là phân giác của $\widehat {CAB}$.

Xem lời giải

Giải bởi Vietjack

Đúng

Do $\Delta ACE = \Delta AKE$ (ch – cgv) nên $\widehat {CAE} = \widehat {KAE}$ (hai góc tương ứng).

Do đó, $AE$ là phân giác của $\widehat {CAB}$.

Câu 3:

c) $EC > EB.$

Xem lời giải

Giải bởi Vietjack

Sai

Do $\Delta ACE = \Delta AKE$ (ch – cgv) nên $CE = EK$ (hai cạnh tương ứng).

Mà xét tam giác $\Delta KEB$ vuông tại $K$ nên $BE > EK$.

Mà $EK = EC$ nên $EB > CE$.

Câu 4:

d) $AB = 2AC.$

Xem lời giải

Giải bởi Vietjack

Đúng

Ta có $\widehat {ABC} = 180^\circ - \left( {\widehat A + \widehat C} \right) = 180^\circ - \left( {90^\circ + 60^\circ } \right) = 30^\circ $.

Lại có $AE$ là phân giác của $\widehat {CAB}$ nên $\widehat {EAK} = \frac{1}{2}\widehat {CAB} = 30^\circ $.

Suy ra $\widehat {EAK} = \widehat {CBA} = 30^\circ $.

Do đó, tam giác $AEB$ cân tại $E$.

Có $EK \bot AB$ nên $EK$ là đường cao, đường trung trực trong tam giác $EKB.$

Do đó, $K$ là trung điểm của $AB$

Suy ra $AK = \frac{1}{2}AB$ hay $AB = 2AK$.

Mà $AK = AC$ nên $AB = 2AC$.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

(0,5 điểm) Bạn An mở ngẫu nhiên một cuốn sách có $315$ trang. Tính xác suất để trang sách bạn An mở được là một số chia hết cho 3.

Xem đáp án

Lời giải

Số trang được đánh số là các số chia hết cho 3 là: $\left( {315 - 3} \right):3 + 1 = 105$ (số)

Do đó, xác suất của biến cố “trang sách bạn An mở được là một số chia hết cho 3” là: $\frac{{105}}{{315}} = \frac{1}{3}$.

Câu 2

Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn

Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.

Với số tiền để mua $60{\rm{ m}}$ vải loại I có thể mua được bao nhiêu mét vải loại II, biết rằng giá tiền vải loại II bằng $120\% $ giá tiền vải loại I.

Xem đáp án

Lời giải

Đáp án: $50$

Gọi $x$ là số mét vải loại II mua được ($x > 0,$ mét)

Vì có cùng số tiền nên số mét vải mỗi loại mua được tỉ lệ nghịch với giá tiền 1 mét, ta có:

$\frac{{60}}{x} = \frac{{120}}{{100}}$ suy ra $x = \frac{{60.100}}{{120}} = 50$ (thỏa mãn).

Vậy số mét vải loại II mua được là $50{\rm{ m}}{\rm{.}}$

Câu 3

Các chuyên gia bóng đá nhận định trong trận bóng đá ngày mai giữa hai đội A và , xác suất thắng của đội A là $45\% $, xác suất thua là $50\% $ và xác suất hòa là $5\% $. Theo nhận định trên, đội bóng nào có khả năng thắng cao hơn?

A. Đội A.

B. Đội B.

C. Khả năng như nhau.

D. Chưa kết luận được.

Lời giải