(0,5 điểm) Trong một hộp gỗ có các thẻ được đánh số từ \(100\) đến \(1{\rm{ }}000\). Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất để thẻ rút ra chia hết cho \(17.\)
(0,5 điểm) Trong một hộp gỗ có các thẻ được đánh số từ \(100\) đến \(1{\rm{ }}000\). Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất để thẻ rút ra chia hết cho \(17.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số các chữ số từ 100 đến \(1{\rm{ }}000\) là \(\left( {1{\rm{ }}000 - 100} \right):1 + 1 = 901\) (số)
Nhận thấy \(100:17 = 5\) dư 15.
Do đó, số có ba chữ số nhỏ nhất chia hết cho 17 là \(17.6 = 102\).
Ta có: \(1{\rm{ }}000:17 = 58\) dư 14.
Do đó, số lớn nhất trong khoảng từ 100 đến \(1{\rm{ }}000\) chia hết cho 17 là: \(58.17 = 986\).
Suy ra, số các chữ số từ 100 đến \(1{\rm{ }}000\) chia hết cho 17 là: \(\left( {58 - 6} \right):1 + 1 = 53\).
Do đó, xác suất rút được thẻ ghi số chia hết cho 17 là: \(\frac{{53}}{{901}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án: \( - 0,5\)
Ta có: \(3x\left( {2x + 1} \right) + \left( {2 - x} \right)\left( {6x + 3} \right) = 0\)
\(6{x^2} + 3x + 12x + 6 - 6{x^2} - 3x = 0\)
\(\left( {6{x^2} - 6{x^2}} \right) + \left( {3x - 3x} \right) + 12x + 6 = 0\)
\(12x + 6 = 0\)
\(12x = - 6\) nên \(x = - \frac{1}{2}\) hay \(x = - 0,5\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án: \(1888\)
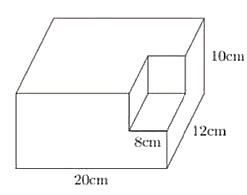
Thể tích khối hộp hình chữ nhật ban đầu là: \(20.12.10 = 2{\rm{ }}400{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Thể tích khối lập phương bị cắt đi là \({8^3} = 512{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).
Do đó, thể tích phần còn lại của khối gỗ là: \(2400 - 512 = 1{\rm{ }}888{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Câu 3
Cho \(\Delta ABC\) có \(I\) là giao điểm của ba đường phân giác trong \(\Delta ABC\). Khi đó, ta có:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập