Câu 1-2. (2,5 điểm)
1. Cho hàm số \(y = f\left( x \right) = - {x^2}.\)
a) Tính \(f\left( 0 \right);f\left( 3 \right)\).
a) Tìm \({x_0}\) biết \(f\left( {{x_0}} \right) = - 27\).
Câu 1-2. (2,5 điểm)
1. Cho hàm số \(y = f\left( x \right) = - {x^2}.\)
a) Tính \(f\left( 0 \right);f\left( 3 \right)\).
a) Tìm \({x_0}\) biết \(f\left( {{x_0}} \right) = - 27\).
Quảng cáo
Trả lời:
1. Xét đồ thị hàm số \(y = f\left( x \right) = - {x^2}.\)
a) Thay \(x = 0\,;\,\,x = 3\) vào hàm số \(y = f\left( x \right) = - {x^2}.\)
\(f\left( 0 \right) = 0\,;\,\,f\left( 3 \right) = - {3^2} = - 9.\)
Vậy \(f\left( 0 \right) = 0\,;\,\,f\left( 3 \right) = - 9.\)
b) Ta có \(y = f\left( x \right) = - {x^2}\) nên \(f\left( {{x_0}} \right) = - {x_0}^2\).
Mà \(f\left( {{x_0}} \right) = - 27\) nên \( - {x_0}^2 = - 27\) hay \({x_0}^2 = 27\).
Do đó \({x_0} = - 3\sqrt 3 \) hoặc \({x_0} = 3\sqrt 3 \).
Vậy khi \(f\left( {{x_0}} \right) = - 27\) thì \({x_0} = - 3\sqrt 3 \) hoặc \({x_0} = 3\sqrt 3 \).
Câu hỏi cùng đoạn
Câu 2:
2. Giải bài toán sau bằng cách lập phương trình:
Quãng đường \({\rm{AB}}\) dài \(90{\rm{\;km}}\), có hai ô tô khởi hành cùng một lúc. Ô tô thứ nhất đi từ A đến \({\rm{B}}\) ô tô thứ hai đi từ \({\rm{B}}\) đến \({\rm{A}}\). Sau \[1\] giờ hai xe gặp nhau và tiếp tục đi. Xe ô tô thứ hai tới A trước xe thứ nhất tới B là \[27\] phút. Tính vận tốc của mỗi xe.
2. Giải bài toán sau bằng cách lập phương trình:
Quãng đường \({\rm{AB}}\) dài \(90{\rm{\;km}}\), có hai ô tô khởi hành cùng một lúc. Ô tô thứ nhất đi từ A đến \({\rm{B}}\) ô tô thứ hai đi từ \({\rm{B}}\) đến \({\rm{A}}\). Sau \[1\] giờ hai xe gặp nhau và tiếp tục đi. Xe ô tô thứ hai tới A trước xe thứ nhất tới B là \[27\] phút. Tính vận tốc của mỗi xe.
2. Đổi 27 phút \( = \frac{9}{{20}}\) (giờ).
Sau 1 giờ hai xe gặp nhau nên tổng vận tốc của hai xe bằng \(90\,\,{\rm{km}}/{\rm{h}}.\)
Gọi \(x\,\,\left( {{\rm{km}}/{\rm{h}}} \right)\) là vận tốc cùa \({\rm{xe}}\) thứ nhất \(\left( {0 < x < 90} \right)\).
thì vận tốc của xe thứ hai là \[90 - x\,\,\left( {{\rm{km}}/{\rm{h}}} \right)\].
Thời gian của xe thứ nhất di từ \({\rm{A}}\) đến \({\rm{B}}\) là \(\frac{{90}}{x}\) (giờ).
Thời gian của xe thứ hai là \(\frac{{90}}{{90 - x}}\) (giờ).
Theo đề bài, ta có phương trình: \(\frac{{90}}{x} - \frac{9}{{90 - x}} = \frac{9}{{20}}\).
\(\frac{{10}}{x} - \frac{1}{{90 - x}} = \frac{1}{{20}}\)
\({x^2} - 490x + 18\,\,000 = 0\)
\(x = 40\) (TMĐK) hoặc \(x = 450\) (loại).
Vậy vận tốc của xe thứ nhất là \[40\,\,{\rm{km}}/{\rm{h}}\]; vận tốc của xe thứ hai là \(50\,\,{\rm{km}}/{\rm{h}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
. a) Từ biểu đồ trên, ta có bảng tần số ghép nhóm tương ứng như sau:
|
Cân nặng (kg) |
\[\left[ {35\,;\,\,40} \right)\] |
\[\left[ {40\,;\,\,45} \right)\] |
\[\left[ {45\,;\,\,50} \right)\] |
\[\left[ {50\,;\,\,55} \right)\] |
\[\left[ {55\,;\,\,60} \right)\] |
\[\left[ {60\,;\,\,65} \right)\] |
|
Tần số tương đối |
5% |
10% |
37,5% |
27,5% |
15% |
5% |
Lời giải
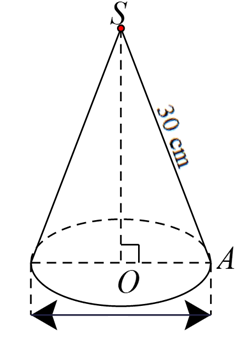
a) Đường kính của hình nón là: \[26 - 2{\rm{ }}.{\rm{ }}3 = 20{\rm{ }}\left( {{\rm{cm}}} \right)\].
Bán kính \[r = \frac{{20}}{2} = 10{\rm{ }}\left( {{\rm{cm}}} \right)\].
Đường sinh là \[30{\rm{ cm}}\].
Vậy diện tích xung quanh của hình nón là:
\[{S_{xq}} = \pi rl = \pi \cdot 10 \cdot 30 = 300\pi {\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right) \approx 942,48{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Để phủ kín mặt ngoài chiếc mũ của chú hề, số giấy màu cần dùng là khoảng \[942,48{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
