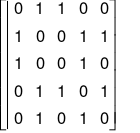Khi xây dựng chu trình Hamilton, nếu lấy hai cạnh liên thuộc với một đỉnh đặt vào chu trình thì:
A. Có thể xóa tất cả các cạnh còn lại không liên thuộc với đỉnh đó.
B. Có thể xóa tất cả các cạnh còn lại liên thuộc với đỉnh đó.
C. Có thể xóa tất cả các cạnh còn lại của đồ thị.
D. Có thể lấy thêm các cạnh liên thuộc với đỉnh đó.
Câu hỏi trong đề: 540 câu trắc nghiệm tổng hợp Toán rời rạc có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn đáp án B
Hot: Đăng kí gói VIP VietJack thi online kèm đáp án chi tiết không giới hạn toàn bộ website (chỉ từ 199k). Đăng kí ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc lẻ
B. Chu trình đi qua tất cả các đỉnh mỗi đỉnh đúng một lần trừ đỉnh bậc chẵn
C. Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
D. Chu trình đi qua tất cả các đỉnh của đồ thị mỗi đỉnh hơn một lần
Lời giải
Chọn đáp án C
Câu 2
A. 5 miền
B. 6 miền
C. 7 miền
D. 8 miền
Lời giải
Chọn đáp án D
Câu 3
A. Euler
B. Hamilton và Euler
C. Hamilton
D. Không liên thông
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hai lần số cạnh.
B. Hai lần số đỉnh.
C. Trung bình cộng của số đỉnh và số cạnh.
D. Tổng của số đỉnh và số cạnh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Đồ thị là liên thông.
B. Đồ thị không liên thông.
C. Tính liên thông của đồ thị không xác định.
D. Đồ thị là liên thông mạnh
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Đồ thị vô hướng hoặc có hướng có trọng số không âm.
B. Đồ thị liên thông có trọng số không âm
C. Đồ thị có hướng có trọng số không âm.
D. Đồ thị vô hướng hoặc có hướng không có chu trình âm
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Thuật toán BFS(u) duyệt tất cả các thành phần liên thông của đồ thị
B. Thuật toán BFS(u) luôn tìm ra được đường đi giữa hai đỉnh bất kì của đồ thị
C. Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị trong cùng thành phần liên thông với đỉnh u
D. Thuật toán BFS(u) duyệt tất cả các đỉnh của đồ thị mỗi đỉnh đúng một lần
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo