Câu hỏi:
21/04/2025 173
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] nhọn \[\left( {AB < AC} \right)\] có hai đường cao \[BE,{\rm{ }}CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
Câu 9-11. (2,5 điểm) Cho tam giác \[ABC\] nhọn \[\left( {AB < AC} \right)\] có hai đường cao \[BE,{\rm{ }}CF\] cắt nhau tại \[H.\]
a) Chứng minh: .
Quảng cáo
Trả lời:
Giải bởi Vietjack
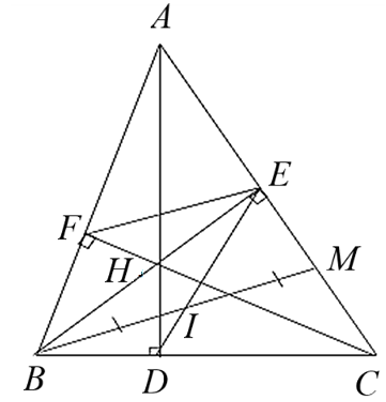
a) Xét \[\Delta FHB\] và \[\Delta EHC\] có:
\[\widehat {FHB} = \widehat {EHC}\]; \(\widehat {HFB} = \widehat {HEC}\;\left( { = 90^\circ } \right)\)
Do đó (g.g).
Câu hỏi cùng đoạn
Câu 2:
b) Chứng minh: \(AF \cdot AB = AE \cdot AC\).
b) Chứng minh: \(AF \cdot AB = AE \cdot AC\).
Lời giải của GV VietJack
b) Xét \[\Delta AEB\] và \[\Delta AFC\] có:
\(\widehat {EAB} = \widehat {FAC}\;\,\left( {\widehat A\;\,{\rm{chung}}} \right)\)
\(\widehat {AEB} = \widehat {AFC}\;\left( { = 90^\circ } \right)\)
Do đóSuy ra \(\frac{{AE}}{{AF}} = \frac{{AB}}{{AC}}\) hay \(AF \cdot AB = AE \cdot AC\) (đpcm)
Câu 3:
c) Đường thẳng qua \[B\] và song song với \[EF\] cắt \[AC\] tại \[M.\] Gọi \[I\] là trung điểm của \[BM,{\rm{ }}D\] là giao điểm của \[EI\] và \[BC.\] Chứng minh ba điểm \[A,{\rm{ }}H,{\rm{ }}D\] thẳng hàng.
c) Đường thẳng qua \[B\] và song song với \[EF\] cắt \[AC\] tại \[M.\] Gọi \[I\] là trung điểm của \[BM,{\rm{ }}D\] là giao điểm của \[EI\] và \[BC.\] Chứng minh ba điểm \[A,{\rm{ }}H,{\rm{ }}D\] thẳng hàng.
Lời giải của GV VietJack
c) Xét \[\Delta ABC\] có hai đường cao \[BE,{\rm{ }}CF\] và cắt nhau tại \[H\] nên suy ra \[H\] là trực tâm của tam giác \[ABC\] nên \[AH \bot BC\]. (1)
Xét \[\Delta BEM\] vuông tại \[E\] có \[I\] là trung điểm của \[BM\] nên \(IE = BI = IM = \frac{{BM}}{2}\).
Xét \[\Delta IEM\] có \[IE = IM\] (cmt) nên tam giác \[IEM\] cân tại \[I\].
Suy ra \(\widehat {IEM} = \widehat {IME}\). (2)
• Xét \[\Delta ABC\] có \[FE{\rm{ // }}BC\] suy ra \(\widehat {AEF} = \widehat {AMB}\) (hai góc đồng vị). (3)
Ta có \[AF \cdot AB = AE \cdot AC\] suy ra \(\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\).
• Xét \[\Delta ABF\] và \[\Delta ABC\] có:
\[\widehat {EAF} = \widehat {BAC}\,\;\left( {\widehat A\;\,{\rm{chung}}} \right)\]; \[\frac{{AF}}{{AC}} = \frac{{AE}}{{AB}}\;\,\left( {{\rm{cmt}}} \right)\]
Do đóSuy ra \(\widehat {AEF} = \widehat {ABC}\) (hai góc tương ứng). (4)
Từ (2), (3), (4) suy ra \(\widehat {CED} = \widehat {ABC}\).
• Xét \[\Delta CED\] và \[\Delta CBA\] có:
\(\widehat {ECD} = \widehat {BCA}\,\;\left( {\widehat C\;\,{\rm{chung}}} \right)\); \(\widehat {CED} = \widehat {ABC}\;\,\left( {{\rm{cmt}}} \right)\)
Do đóSuy ra \(\frac{{CE}}{{CB}} = \frac{{CD}}{{CA}}\) hay \(\frac{{CE}}{{CD}} = \frac{{CB}}{{CA}}\).
• Xét \[\Delta CEB\] và \[\Delta CDA\] có:
\(\frac{{CE}}{{CD}} = \frac{{CB}}{{CA}}\;\,\left( {{\rm{cmt}}} \right)\); \(\widehat {ECB} = \widehat {DCA}\,\;\left( {\widehat C\;\,{\rm{chung}}} \right)\)
Do đóSuy ra \(\widehat {CDA} = \widehat {CEB}\) (hai góc tương ứng).
Nên \(\widehat {CDA} = 90^\circ \), do đó \(AD \bot BC\). (5)
Từ (1) và (5) suy ra ba điểm \[A,{\rm{ }}H,{\rm{ }}D\] thẳng hàng (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Tổng số sản phẩm loại A và loại B là \(10 + 7 = 17\) (sản phẩm).
Khi lấy ngẫu nhiên 2 sản phẩm:
Chọn sản phẩm thứ nhất chọn 1 trong 17 sản phẩm nên có 17 cách;
Chiếc sản phẩm thứ hai chọn \[1\] trong 16 sản phẩm còn lại nên có 16 cách.
Số cách chọn 2 sản phẩm trong số 17 sản phẩm là: \(\frac{{17.16}}{2} = 136\) (cách) (cứ mỗi cặp bị lặp lại 2 lần).
Có \(\frac{{10.9}}{2} = 45\) cách chọn chỉ lấy ra 2 sản phẩm loại A.
Số kết quả thuận lợi của biến cố E là \[136--45 = 91.\]
Vậy xác suất của biến cố E là \(\frac{{91}}{{136}}\).
Lời giải
a) Điều kiện xác định của biểu thức \(P\) là \(9 - {x^2} \ne 0,\) \(x + 3 \ne 0\) hay \[x \ne 3,\,\,x \ne - 3\].
Vậy điều kiện xác định của biểu thức \(P\) là \[x \ne 3,\,\,x \ne - 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận