Câu hỏi:
21/04/2025 132
Câu 12-13. (1,5 điểm)
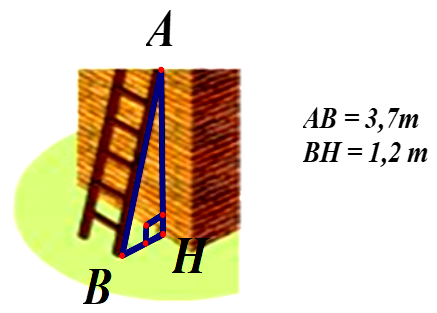
Một chiếc thang có chiều dài \[AB = 3,7\,\,{\rm{m}}\] đặt cách một bức tường khoảng cách \[BH = 1,2\,\,{\rm{m}}.\] Biết rằng khoảng cách “an toàn” khi \(2,0 < \frac{{AH}}{{BH}} < 2,2\) (xem hình vẽ). Tính chiều cao \[AH.\] Từ đó kiểm tra xem khoảng cách đặt thang cách chân tường là \[BH\] có “an toàn” không?
Câu 12-13. (1,5 điểm)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng định lí Pythagore vào tam giác \[ABH\] vuông tại \[H\], ta có:
\(A{B^2} = A{H^2} + B{H^2}\) suy ra \(A{H^2} = A{B^2} - B{H^2}\).
Do đó \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{{\left( {3,7} \right)}^2} - {{\left( {1,2} \right)}^2}} = 3,5\,\,(m)\).
Ta có \(\frac{{AH}}{{BH}} = \frac{{3,5}}{{1,2}} \approx 2,9\).
Mà \[2,9 > 2,2\] nên khoảng cách đặt thang cách chân tường là không an toàn.
Câu hỏi cùng đoạn
Câu 2:
Một hộp quà có dạng là một hình chóp tứ giác đều có cạnh đáy bằng \(10\,\,{\rm{cm}}\), trung đoạn bằng \(13\,\,{\rm{cm}}\). Tính chiều cao của hộp quà.
Một hộp quà có dạng là một hình chóp tứ giác đều có cạnh đáy bằng \(10\,\,{\rm{cm}}\), trung đoạn bằng \(13\,\,{\rm{cm}}\). Tính chiều cao của hộp quà.
Lời giải của GV VietJack
Ta có \(SE\) là trung đoạn nên \(E\) là trung điểm của \(AB\).
Xét \(\Delta ABD\) có \(E,\,\,H\) lần lượt là trung điểm của \(AB,\,BD.\)
Suy ra \(EH\) là đường trung bình của \(\Delta ABD\) nên \(EH = \frac{1}{2}AD = 5\,\,({\rm{cm)}}\).
Áp dụng định lí Pythagore \(\Delta SEH\) vuông tại \(H\) có: \(S{E^2} = S{H^2} + E{H^2}\)Suy ra \(S{H^2} = S{E^2} - E{H^2} = {13^2} - {5^2}\)
Do đó \(SH = 12\,\,{\rm{cm}}\).
Vậy chiều cao của hộp quà là 12 cm.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Tổng số sản phẩm loại A và loại B là \(10 + 7 = 17\) (sản phẩm).
Khi lấy ngẫu nhiên 2 sản phẩm:
Chọn sản phẩm thứ nhất chọn 1 trong 17 sản phẩm nên có 17 cách;
Chiếc sản phẩm thứ hai chọn \[1\] trong 16 sản phẩm còn lại nên có 16 cách.
Số cách chọn 2 sản phẩm trong số 17 sản phẩm là: \(\frac{{17.16}}{2} = 136\) (cách) (cứ mỗi cặp bị lặp lại 2 lần).
Có \(\frac{{10.9}}{2} = 45\) cách chọn chỉ lấy ra 2 sản phẩm loại A.
Số kết quả thuận lợi của biến cố E là \[136--45 = 91.\]
Vậy xác suất của biến cố E là \(\frac{{91}}{{136}}\).
Lời giải
a) Điều kiện xác định của biểu thức \(P\) là \(9 - {x^2} \ne 0,\) \(x + 3 \ne 0\) hay \[x \ne 3,\,\,x \ne - 3\].
Vậy điều kiện xác định của biểu thức \(P\) là \[x \ne 3,\,\,x \ne - 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận