Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao \(21{\rm{ m,}}\) độ dài cạnh đáy là \(34{\rm{ m}}\).
Tính tổng diện tích của các tấm kính để phủ kín bốn mặt bên của bảo tàng này (đơn vị: m2).
(Các kết quả làm tròn đến hàng đơn vị)
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao \(21{\rm{ m,}}\) độ dài cạnh đáy là \(34{\rm{ m}}\).
Tính tổng diện tích của các tấm kính để phủ kín bốn mặt bên của bảo tàng này (đơn vị: m2).
(Các kết quả làm tròn đến hàng đơn vị)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: \(1836\)
Ta minh họa bảo tàng bằng hình chóp tứ giác sau:
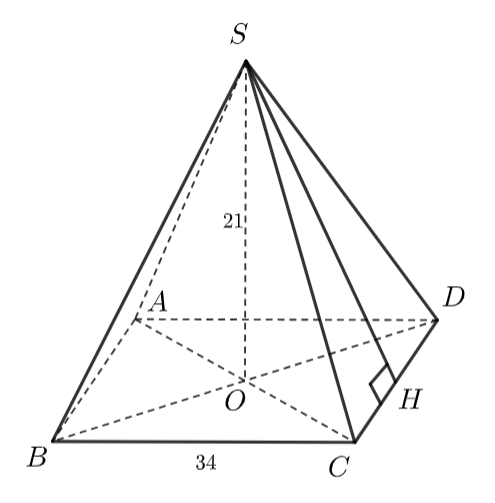
Đường cao của hình chóp \(SO\) vuông góc với mặt đáy \(ABCD\) nên \(SO \bot OH.\)
Dễ thấy \(OH = \frac{1}{2}DC = \frac{1}{2}.34 = 17{\rm{ }}\left( {\rm{m}} \right)\)
Xét tam giác \(SOH\) vuông tại \(O.\)
Theo định lí Pythagore, ta có: \(S{H^2} = S{O^2} + O{H^2}\)
Suy ra \(S{H^2} = {21^2} + {17^2} = 730\)
Suy ra \(SH = \sqrt {730} \approx 27{\rm{ }}\left( {\rm{m}} \right)\).
Nửa chu vi mặt đáy là: \(P = \frac{1}{2}\left( {34 + 34 + 34 + 34} \right) = 68{\rm{ }}\left( {\rm{m}} \right)\)
Tổng diện tích các tấm kính để phủ kín bốn mặt bên của bảo tàng hình chóp này là:
\({S_{xq}} = P.d = 68.27 = 1836{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
Điều kiện xác định của phân thức \(\frac{{x - 1}}{{x - 2}}\) là \(x - 2 \ne 0\) hay \(x \ne 2.\)
Lời giải
Hướng dẫn giải
Ta có: \[1 - \frac{1}{{{k^2}}} = \frac{{{k^2} - 1}}{{{k^2}}} = \frac{{\left( {k - 1} \right)\left( {k + 1} \right)}}{{{k^2}}}\].
Do đó, ta có: \[C = \left( {1 - \frac{1}{{{2^2}}}} \right).\left( {1 - \frac{1}{{{3^2}}}} \right).\left( {1 - \frac{1}{{{4^2}}}} \right).....\left( {1 - \frac{1}{{{n^2}}}} \right)\]
\[C = \frac{{1.3}}{{{2^2}}}.\frac{{2.4}}{{{3^2}}}.\frac{{3.5}}{{{4^2}}}....\frac{{\left( {n - 1} \right)\left( {n + 1} \right)}}{{{n^2}}}\]
\[C = \frac{{1.3.2.4.3.5.....\left( {n - 1} \right)\left( {n + 1} \right)}}{{{2^2}{{.3}^2}{{.4}^2}.....{n^2}}}\]
\[C = \frac{{1.2.3.....\left( {n - 1} \right)}}{{2.3.4.....\left( {n - 1} \right)n}}.\frac{{3.4.5.....\left( {n + 1} \right)}}{{2.3.4....n}}\]
\[C = \frac{1}{n}.\frac{{n + 1}}{2} = \frac{{n + 1}}{{2n}}\].
Vậy \[C = \frac{{n + 1}}{{2n}}.\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập