khoahoc.vietjack.com
Giảm 50% Kích hoạt VIP
khoahoc.vietjack.com
Kích hoạt VIP Đăng nhập
Tạo VIP
  2. Phòng luyện thi ĐGNL - ĐGTD
  3. ĐHQG Hồ Chí Minh

Câu hỏi:

12/03/2026 404 Lưu

Dựa vào thông tin dưới đây để trả lời các câu từ 84 đến 86

Cho hình chóp tứ giác \(S.ABCD\) có đáy ABCD là hình thoi cạnh 2a, \(SA = a,SB = a\sqrt 3 \), \(\widehat {BAD} = 60^\circ \) và mặt phẳng \(\left( {SAB} \right)\) vuông góc với mặt đáy. Gọi \({\rm{M}},{\rm{N}}\), K lần lượt là trung điểm của AB, BC, AD.

Thể tích khối tứ diện NSDC là:     

A. \(\frac{{3{a^3}}}{4}\).                       
B. \(\frac{{{a^3}}}{{12}}\).                             
C. \(\frac{{{a^3}}}{4}\).  
D. \(\frac{{{a^3}}}{3}\).
Xem lời giải

Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 26) !!

Flashcard Bắt Đầu Thi Giao bài

Quảng cáo

Trả lời:

verified Giải bởi Vietjack

Từ \[AB = 2a,\,\,SA = a,\,\,SB = a\sqrt 3 \Rightarrow \Delta SAB\] vuông tại S.

Kẻ \(SH \bot AB\) tại H, do \(\left( {{\rm{SAB}}} \right) \bot \left( {{\rm{ABCD}}} \right)\) nên \({\rm{SH}} \bot \left( {{\rm{ABCD}}} \right)\).

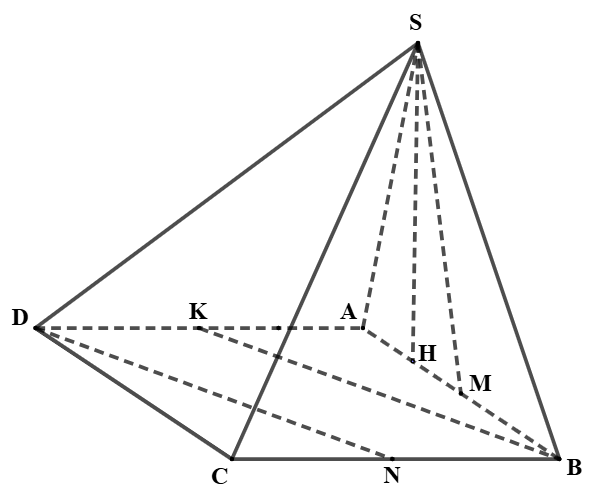
Thể tích khối tứ diện NSDC là: (ảnh 1) 

Ta có \(SH = \frac{{SA \cdot SB}}{{AB}} = \frac{{a \cdot a\sqrt 3 }}{{2a}} = \frac{{a\sqrt 3 }}{2}\).

Mặt khác \({S_{CDN}} = \frac{1}{2} \cdot CD \cdot CN \cdot \sin \widehat {DCN} = \frac{1}{2} \cdot 2a \cdot a \cdot {\rm{sin}}60^\circ = \frac{{{a^2}\sqrt 3 }}{2}\).

Do vậy \({V_{{\rm{NSDC\;}}}} = {V_{S.CDN}} = \frac{1}{3} \cdot {S_{CDN}} \cdot SH = \frac{1}{3} \cdot \frac{{{a^2}\sqrt 3 }}{2} \cdot \frac{{a\sqrt 3 }}{2} = \frac{{{a^3}}}{4}\). Chọn C.

Câu hỏi cùng đoạn

Câu 2:

Độ dài đoạn thẳng BK bằng    

A. \(2a\).                  
B. \(\frac{1}{3}a\).  
C. \(a\sqrt 3 \). 
D. \(\frac{1}{2}a\).

Xem lời giải

verified Giải bởi Vietjack

Ta có \[B{K^2} = B{A^2} + A{K^2} - 2 \cdot BA \cdot AK \cdot {\rm{cos}}\widehat {BAK} = 3{a^2} \Rightarrow BK = a\sqrt 3 \]. Chọn C.

Câu 3:

Côsin của góc giữa hai đường thẳng SM và DN là:     

A. \(\frac{{\sqrt 3 }}{4}\).                       
B. \(\frac{2}{3}\).            
C. \(\frac{{\sqrt 2 }}{2}\).                         
D. \(\frac{1}{5}\).

Xem lời giải

verified Giải bởi Vietjack

Do tam giác SAB vuông tại S nên \(SM = \frac{1}{2}AB = a\).

Gọi L là trung điểm AK, I là trung điểm ML.

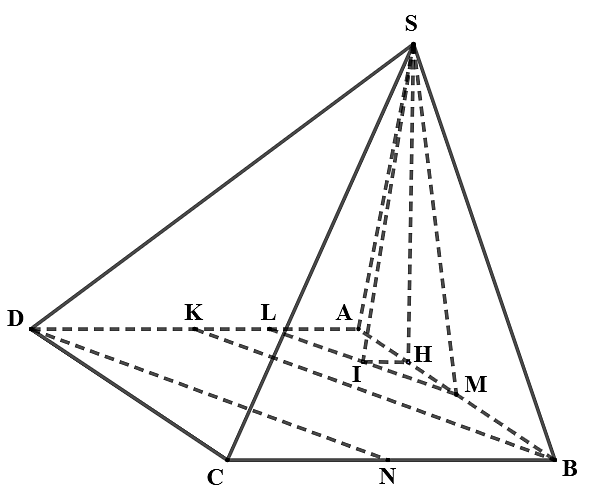
Côsin của góc giữa hai đường thẳng SM và DN là: (ảnh 1) 

Ta thấy \(B{K^2} + A{K^2} = 3{a^2} + {a^2} = 4{a^2} = A{B^2}\) nên tam giác ABK vuông tại K.

\( \Rightarrow BK \bot AD \Rightarrow ML \bot AD \Rightarrow ML \bot HI\).

Từ \(ML \bot HI\) và \(ML \bot SH \Rightarrow ML \bot SI\). Do đó: \({\rm{cos}}\,\widehat {SML} = \frac{{MI}}{{SM}} = \frac{{ML}}{{2SM}} = \frac{{BK}}{{4SM}} = \frac{{\sqrt 3 }}{4}\).

Vì \(ML{\rm{//}}\,BK{\rm{//}}\,DN\) nên \(\left( {SM\,,\,DN} \right) = \left( {SM\,,\,ML} \right) = \widehat {SML}\). Chọn A.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

  • Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
  • Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
  • Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
  • Tải xuống đề thi [DOCX] với đầy đủ đáp án
  • Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
  • Bao gồm tất cả các bậc từ Tiểu học đến Đại học
  • Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
  • Đăng ký ngay
Avatar

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Xác suất để thí sinh được chọn lọt vào vòng bán kết là:     
A. \[0,3\].                 
B. \[0,15\].               
C. \(0,2\).                          
D. \(0,25\).

Lời giải

Gọi A, B, C lần lượt là biến cố thí sinh được chọn lọt vào vòng sơ khảo, vòng bán kết và vòng chung kết.

Vì có 50% thí sinh lọt vào vòng sơ khảo nên \(P\left( A \right) = 0,5\).

Vì có 30% thí sinh của vòng sơ khảo được chọn để vào vòng bán kết nên \(P\left( {B|A} \right) = 0,3\).

Khi đó, xác suất để thí sinh lọt vào vòng bán kết là:

\(P\left( B \right) = P\left( {AB} \right) = P\left( {B|A} \right) \cdot P\left( A \right) = 0,3 \cdot 0,5 = 0,15\). Chọn B.

Câu 2

Đồ thị của hàm số đã cho có tiệm cận xiên là đường thẳng    
A. \[y = x + 1\].       
B. \(y = x - 1\).        
C. \[y = x + 2\].                               
D. \(y = x - 2\).

Lời giải

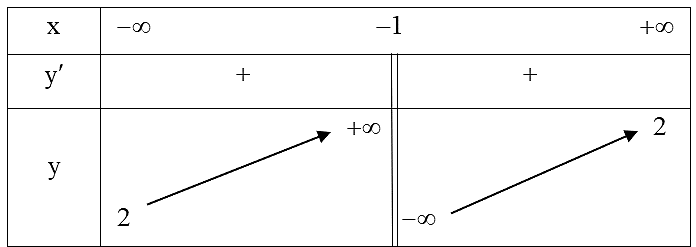
Nhìn đồ thị ta thấy đồ thị hàm số có đường tiệm cận xiên đi qua hai điểm \(M\left( { - 1\,;0} \right),N\left( {0\,;1} \right)\) nên có phương trình: \(y = x + 1\). Chọn A.

Câu 3

Tọa độ giao điểm \(A\) của của đường thẳng d với mặt phẳng \(\left( P \right)\) là:     
A. 0 ; 0; 2
B. 0 ; 0; - 2
C. \(\left( {0\,;\,0;\,3} \right)\).                      
D. 0 ; 0; - 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tập nghiệm của bất phương trình \({\left( {\frac{1}{8}} \right)^{x - 1}} \ge 128\) là:    
A. \(\left( { - \infty ;\frac{8}{3}} \right]\).                  
B. \(\left[ {\frac{1}{8}; + \infty } \right)\).                
C. \(\left( { - \infty ; - \frac{4}{3}} \right]\).                               
D. \(\left( { - \infty ; - \frac{{10}}{3}} \right]\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:

c (ảnh 1) 

Số giá trị nguyên của \(b \in \left[ { - 2;3} \right]\) là:    
A. \(6\).                    
B. \(3\).                    
C. \(4\).                             
D. \(5\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đường thẳng \(x = k\) chia hình phẳng \(D\) thành hai phần có diện tích bằng nhau. Khi đó:    
A. \[k \in \left( { - 2\,; - 1} \right)\].       
B. \[k \in \left( { - 1\,;\,0} \right)\].          
C. \(k \in \left( {0\,;\,1} \right)\).                      
D. \(k \in \left( {1\,;\,2} \right)\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Nghiệm dương bé nhất của phương trình \(f\left( x \right) = 0\) là:    
A. \[\frac{\pi }{4}\].                                
B. \[\frac{\pi }{3}\].    
C. \[\pi \].                
D. \(\frac{\pi }{2}\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Đăng ký

Bạn đã có tài khoản?

Khóa học 1 - 12
THPT
THCS
Phòng luyện đề
ĐGNL - ĐGTD
Tốt nghiệp THPT
Ôn vào 10
Ôn vào 6
Tài liệu
THPT
THCS
Tin Tuyển Sinh
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập