Dựa vào thông tin dưới đây để trả lời các câu từ 83 đến 84
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\) và m là tham số thực.
Số giá trị nguyên dương của tham số m để hàm số có tất cả 3 cực trị là:
Dựa vào thông tin dưới đây để trả lời các câu từ 83 đến 84
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right)\) với mọi \(x \in \mathbb{R}\) và m là tham số thực.
Câu hỏi trong đề: Đề thi ĐGNL ĐHQG Hồ Chí Minh (V-ACT) năm 2026-2027 (Đề 29) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Để hàm số có 3 cực trị thì \(f'\left( x \right) = 0\) phải có 3 nghiệm bội lẻ.
\(f'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right) = 0\) có 3 nghiệm bội lẻ.
\( \Leftrightarrow {x^2} - 6x + m = 0\) có hai nghiệm phân biệt khác 2\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{\Delta '}} = 9 - m > 0}\\{{2^2} - 6 \cdot 2 + m \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < 9}\\{m \ne 8}\end{array}} \right.} \right.\).
Vậy có 7 giá trị nguyên dương của \(m\) thoả mãn. Chọn C.
Câu hỏi cùng đoạn
Câu 2:
Số giá trị nguyên m thuộc đoạn \(\left[ { - 20;20} \right]\) để hàm số \(g\left( x \right) = f\left( {1 - x} \right)\) nghịch trên khoảng \(\left( { - \infty ; - 1} \right)\) là:
Giải bởi Vietjack
Ta có \(g'\left( x \right) = f'\left( {1 - x} \right) = - {\left( {1 - x} \right)^2}\left( { - x - 1} \right)\left[ {{{\left( {1 - x} \right)}^2} - 6\left( {1 - x} \right) + m} \right]\)
\( = {\left( {x - 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m - 5} \right)\).
Hàm số \(g\left( x \right)\) nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\)
\( \Leftrightarrow g'\left( x \right) \le 0,\forall x < - 1\,\,\left( {\rm{*}} \right)\), (dấu = xảy ra tại hữu hạn điểm).
Với \(x < - 1\) thì \({\left( {x - 1} \right)^2} > 0\) và \(x + 1 < 0\) nên
\(\left( {\rm{*}} \right) \Leftrightarrow {x^2} + 4x + m - 5 \ge 0,\forall x < - 1\)\( \Leftrightarrow m \ge - {x^2} - 4x + 5,\forall x < - 1\).
Xét hàm số \(y = - {x^2} - 4x + 5\) trên khoảng \(\left( { - \infty ; - 1} \right)\), ta có bảng biến thiên:
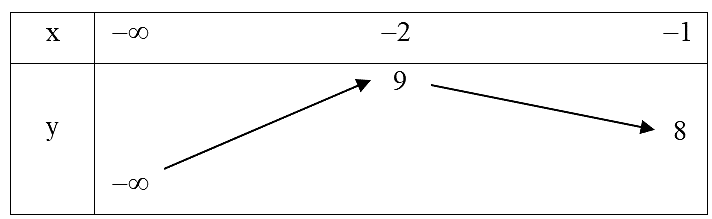
Từ bảng biến thiên suy ra \(m \ge 9\).
Kết hợp với \(m\) thuộc đoạn \(\left[ { - 20;20} \right]\) và \(m\) nguyên nên \(m \in \left\{ {9;10;11; \ldots ;20} \right\}\).
Vậy có 12 số nguyên \(m\) thỏa mãn đề bài. Chọn D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Do có 70% khách hàng mua bảo hiểm cho nhiều hơn một chiếc xe nên \(P\left( A \right) = 0,7\).
Suy ra \(P\left( {\bar A} \right) = 1 - P\left( A \right) = 1 - 0,7 = 0,3\). Chọn B.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(\left( C \right)\)là đường tròn giao tuyến của mặt phẳng \(\left( P \right)\) và mặt cầu \(\left( S \right)\).
Gọi \(H\) là hình chiếu của \(I\) lên mặt phẳng \(\left( P \right)\). Ta có \(H\) là tâm đường tròn \(\left( C \right)\) và \(IH = d\left( {I,\left( P \right)} \right) = 2\).
Mặt cầu \(\left( S \right)\) có bán kính \(R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {3^2} - 5} = 3\).Bán kính đường tròn \(\left( C \right)\): \(r = \sqrt {{R^2} - I{H^2}} = \sqrt {{3^2} - {2^2}} = \sqrt 5 \).
Chu vi đường tròn \(\left( C \right)\): \(C = 2\pi \sqrt 5 \). Chọn B.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập