Tìm tất cả các giá trị của tham số \(m\) để phương trình \({(7 - 3\sqrt 5 )^{{x^2}}} + m{(7 + \sqrt 5 )^{{x^2}}} = {2^{{x^2} - 1}}\) có đúng bốn nghiệm phân biệt.
Quảng cáo
Trả lời:
Đáp án D
Hướng dẫn giải
Ta có: \(\left( {7 + 3\sqrt 5 } \right)\left( {7 - 3\sqrt 5 } \right) = 49 - 45 = 4 \Rightarrow 7 + 3\sqrt 5 = \frac{4}{{7 - 3\sqrt 5 }}\).
\( \Rightarrow {(7 - 3\sqrt 5 )^{{x^2}}} + m{(7 + 3\sqrt 5 )^{{x^2}}} = {2^{{x^2} - 1}}\)
\( \Leftrightarrow {\left( {\frac{4}{{7 + 3\sqrt 5 }}} \right)^{{x^2}}} + m{(7 + 3\sqrt 5 )^{{x^2}}} = \frac{1}{2}{.2^{{x^2}}}\)
\( \Leftrightarrow {2.2^{2{x^2}}} - {2^{{x^2}}}.{(7 + 3\sqrt 5 )^2} + 2m{(7 + 3\sqrt 5 )^{2{x^2}}} = 0\)
\( \Leftrightarrow 2.{\left( {\frac{2}{{7 + 3\sqrt 5 }}} \right)^{2{x^2}}} - {\left( {\frac{2}{{7 + 3\sqrt 5 }}} \right)^{{x^2}}} + 2m = 0\) (*)
Đặt \({\left( {\frac{2}{{7 + 3\sqrt 5 }}} \right)^{{x^2}}} = t = > {x^2} = {\rm{lo}}{{\rm{g}}_{\frac{2}{{7 + 3\sqrt 5 }}}}t\).
Ta có: \(0 < \frac{2}{{7 + 3\sqrt 5 }} < 1 \Rightarrow {\rm{lo}}{{\rm{g}}_{\frac{2}{{7 + 3\sqrt 5 }}}}{\rm{t}} > 0 \Leftrightarrow 0 < {\rm{t}} < 1\).
\( \Rightarrow (*) \Leftrightarrow 2{t^2} - t + 2m = 0\)
Để phương trình (*) có 4 nghiệm phân biệt \( \Leftrightarrow pt\left( 1 \right)\) có hai nghiệm phân biệt \(t \in \left( {0;1} \right)\).
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{\Delta }} > 0}\\{af\left( 0 \right) > 0}\\{af\left( 1 \right) > 0}\\{0 < - \frac{b}{{2a}} < 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 - 16m > 0}\\{4m > 0}\\{2\left( {2m + 1} \right) > 0}\\{0 < \frac{1}{2} < 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m < \frac{1}{{16}}}\\{m > 0}\\{m > - \frac{1}{2}}\end{array} \Leftrightarrow 0 < m < \frac{1}{{16}}} \right.} \right.} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án A
Hướng dẫn giải
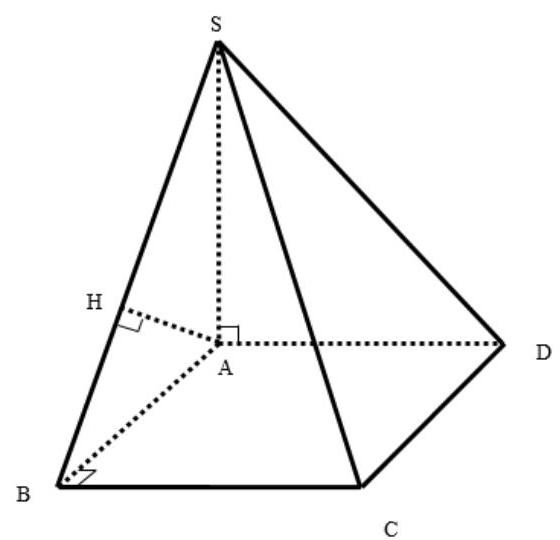
Vì \(AD//BC\) nên \(d\left( {AD,SC} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\).
Ta có:
\({\rm{BC}} \bot {\rm{AB}}\) (do ABCD là hình vuông).
\(SA \bot BC\,\,\left( {do\,\,SA \bot \left( {ABCD} \right)} \right)\).
\( \Rightarrow {\rm{BC}} \bot \left( {{\rm{SAC}}} \right)\).
Trong tam giác SAB, kẻ \({\rm{AH}} \bot {\rm{SB}}\)
Mà: \({\rm{BC}} \bot \left( {{\rm{SAB}}} \right) \Rightarrow {\rm{BC}} \bot {\rm{AH}}\)
\( \Rightarrow {\rm{AH}} \bot \left( {{\rm{SBC}}} \right) \Rightarrow {\rm{d}}\left( {{\rm{A}},\left( {{\rm{SBC}}} \right)} \right) = {\rm{AH}}\).
Xét tam giác SAB vuông tại A, có AH là đường cao:
\(\frac{1}{{{\rm{A}}{{\rm{B}}^2}}} + \frac{1}{{{\rm{S}}{{\rm{A}}^2}}} = \frac{1}{{{\rm{A}}{{\rm{H}}^2}}} \Rightarrow {\rm{AH}} = \frac{{2{\rm{a}}\sqrt 6 }}{3}\).
Vậy khoảng cách giữa hai đường thẳng AD và SC bằng \(\frac{{2{\rm{a}}\sqrt 6 }}{3}\).
Câu 2
A. Cuộc sống đầy khó khăn, vất vả, gian nan.
B. Cuộc sống an nhàn, thanh bình.
C. Cuộc sống chỉ có niềm vui, hạnh phúc.
Lời giải
Đáp án A
Hướng dẫn giải
- Từ "phong trần" trong đoạn thơ "Bắt phong trần phải phong trần" mang một nghĩa biểu tượng, chỉ cuộc sống đầy khó khăn, gian nan và thử thách. Để hiểu rõ hơn, ta có thể phân tích các yếu tố của từ này: "Phong": là gió, tượng trưng cho những tác động bên ngoài, những khó khăn, thử thách mà con người phải đối mặt trong cuộc sống. "Trần": là bụi bặm, sự mệt mỏi, vất vả của cuộc sống. "Trần" ở đây cũng có thể ám chỉ sự hạ giới, đời sống không thanh cao mà phải chịu những điều khổ cực.
- Khi kết hợp lại, "phong trần" chỉ cuộc sống mà con người phải trải qua bao nhiêu khó khăn, vất vả, gian truân và thử thách. Đây là một khái niệm phổ biến trong văn học cổ điển Việt Nam, mang ý nghĩa nhấn mạnh rằng mỗi người phải vượt qua những gian khổ, chông gai trong cuộc sống để đạt được điều gì đó quý giá, như sự thanh cao hay phẩm hạnh.
- Trong câu "Bắt phong trần phải phong trần", tác giả muốn nhấn mạnh rằng, số phận của con người đã được định đoạt, phải trải qua những khó khăn, gian nan (phong trần) để có thể đạt được phần thưởng xứng đáng, ví dụ như sự thanh cao về đạo đức, nhân cách.
- Do đó, "phong trần" không chỉ là những khó khăn bên ngoài mà còn thể hiện một phần trong quá trình rèn luyện, thử thách con người để đạt được sự hoàn thiện trong tâm hồn và nhân cách.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Lục Vân Tiên (Nguyễn Đình Chiểu), Vang bóng một thời (Hoàng Xuân Hãn), Đoạn tuyệt (Nguyễn Công Hoan).
B. Đoạn tuyệt (Nguyễn Công Hoan), Tắt đèn (Ngô Tất Tố), Số đỏ (Vũ Trọng Phụng).
C. Đây thôn Vĩ Dạ (Hàn Mặc Tử), Lão Hạc (Nam Cao), Mưa xuân (Thế Lữ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Its academic excellence and long history.
B. Its location in Cambridge, Massachusetts.
C. Its large student population.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Truyện Kiều.
B. Nhật ký trong tù.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Carbonated soft drinks are healthy and good for hydration.
B. Carbonated soft drinks have several harmful effects on health.
C. Carbonated soft drinks are popular beverages around the world.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.