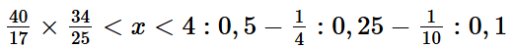a) Cho tam giác ABC, trên cạnh AC lấy diểm K sao cho AK= AC, trên cạnh AB lấy điểm I sao cho AI = AB. Nối IC và BK cắt nhau tại O. So sánh diện tích tam giác ABK và diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
c) Biết IC = 32 cm, tính độ dài đoạn thẳng OC.
a) Cho tam giác ABC, trên cạnh AC lấy diểm K sao cho AK= AC, trên cạnh AB lấy điểm I sao cho AI = AB. Nối IC và BK cắt nhau tại O. So sánh diện tích tam giác ABK và diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
c) Biết IC = 32 cm, tính độ dài đoạn thẳng OC.
Quảng cáo
Trả lời:
Phương pháp
- Muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
- Tìm mối liên hệ giữa đoạn thẳng IO, OC với đoạn thẳng IC dựa vào mối liên hệ giữa diện tích các hình tam giác chứa các cạnh đó. Sau đó tính độ dài đoạn thẳng IO, OC.
Lời giải
Ta có hình vẽ:
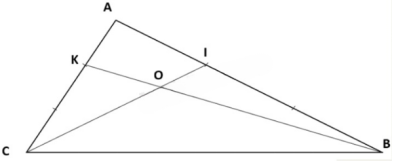
a) Kẻ đường cao BH từ B vuông góc với cạnh CA tại H.
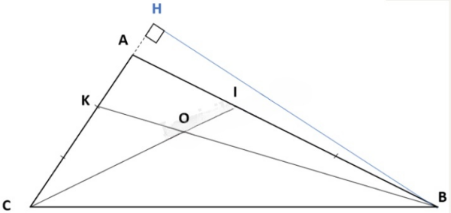
Ta có:
Diện tích tam giác ABK là: = AK × BH : 2
Theo đề ra, AK = AC hay KC = 2 × AK
Diện tích tam giác BCK là: = AK x BH
Vậy diện tích tam giác ABK bằng diện tích tam giác BCK
Vậy diện tích tam giác ABK bé hơn diện tích tam giác BCK.
b) Biết IC = 32 cm, tính độ dài đoạn thẳng IO.
Theo câu a), diện tích tam giác ABK bằng diện tích tam giác BCK = diện tích tam giác ABC
Tương tự câu a), kẻ đường cao từ đỉnh C và vuông góc với cạnh BC.
Diện tích tam giác ACI bằng diện tích tam giác ICB = diện tích tam giác ABC
Vậy diện tích tam giác ABK = Diện tích tam giác ACI (đều bằng diện tích tam giác ABC)
Vậy diện tích tam giác KOC = Diện tích tam giác IOB (đều bằng ![]() diện tích tam giác ABC – diện tích tứ giác OKAI)
diện tích tam giác ABC – diện tích tứ giác OKAI)
- Nối A với O
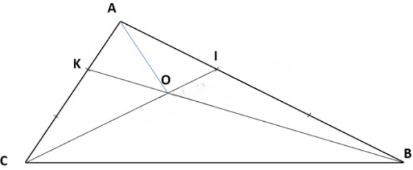
Diện tích tam giác OAK = diện tích tam giác KOC (Xét diện tích tam giác OAK và tam giác OKC có chung đường cao kẻ từ đỉnh O vuông góc với cạnh AC và cạnh đáy AK = KC)
Diện tích tam giác IOA = diện tích tam giác IOB (Xét diện tích tam giác IOA và tam giác IOB có chung đường cao kẻ từ đỉnh O vuông góc với cạnh AB và cạnh đáy AI = IB)
Vậy diện tích tam giác OAK = diện tích tam giác IOA (Vì diện tích tam giác KOC = diện tích tam giác IOB)
Ta có: Diện tích tam giác IOA = diện tích tam giác AOC (Vì diện tích tam giác KOC = diện tích tam giác IOB = diện tích tam giác KOC)
Xét tam giác IOA và tam giác AOC đều có chiều cao kẻ từ đỉnh A đến cạnh OC.
Vậy độ dài đáy IO = OC. Hay IO = IC
Vậy độ dài IO là:
32 × = 8 (cm)
c) Theo câu b, ta có độ dài IO = OC; IO = 8 cm
Vậy độ dài OC là:
8 : = 24 (cm)
Đáp số: a) diện tích tam giác ABK bé hơn diện tích tam giác BCK
b) 8 cm
c) 24 cm
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp
- Diện tích mảnh vườn hình chữ nhật = Chiều dài × Chiều rộng
- Diện tích bồn hoa hình tròn = Bán kính × Bán kính × 3,14
- Diện tích phần đất trồng rau = Diện tích mảnh vườn hình chữ nhật - Diện tích bồn hoa hình tròn – Diện tích lối đi
Lời giải
Diện tích mảnh vườn hình chữ nhật là:
10 × 8 = 80 (m2)
Diện tích bồn hoa hình tròn là:
x 3,14 = 12,56 (m2)
Diện tích phần đất trồng rau là:
80 - 12,56 – 10 = 57,44 (m2)
Đáp án: A
Lời giải
Phương pháp
- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4.
- Muốn chia một số cho 0,1 ta chỉ việc nhân số đó với 10.
- Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2.
Lời giải
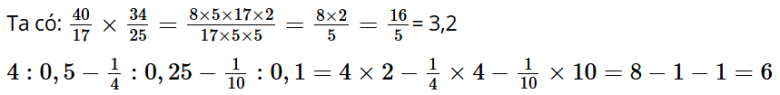
Vậy 3,2 < x < 6
x là số tự nhiên nên x = 4 hoặc x = 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. 4 000 đồng
B. 10 000 đồng
C. 5 000 đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 56 180 000 đồng
B. 56 000 000 đồng
C. 6 180 000 đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.