Câu hỏi:
16/06/2025 119
Sử dụng các thông tin sau cho Câu 5 và Câu 6: Người ta thường tính toán tuổi của các thiên thạch hay mẫu vật dựa vào độ phóng xạ của nó hay tỉ lệ giữa nó với các nguyên tố được tạo ra. Trong tình huống này ta xem xét một mẫu đá Mặt trăng có tỉ lệ số nguyên tử \(_{18}^{40}{\rm{Ar}}\) (bền) và số nguyên tử \(_{19}^{40}\;{\rm{K}}\) trong mẫu là 10,3. Cho rằng các nguyên tử \(_{18}^{40}{\rm{Ar}}\) được tạo ra bởi sự phóng xạ của \(_{19}^{40}\;{\rm{K}}\), chu kỳ bán rã của \(_{19}^{40}\;{\rm{K}}\) là 1,251 tỉ năm. Biết 1 năm có 365 ngày, 1 ngày 24 giờ.
Phân rã của \(_{19}^{40}\;{\rm{K}}\) là phân rã \({\beta ^ + }\)phát ra tia gamma và một neutrino. Một nguyên tử \(_{19}^{40}\;{\rm{K}}\) phân rã sẽ tỏa ra năng lượng cỡ \({{\rm{E}}_1} = 4,6{\rm{MeV}}\). Tính năng lượng tỏa ra trong 1 s của một mẫu vật tính theo đơn vị \(\mu {\rm{J}}\) (làm tròn kết quả đến chữ số hàng phần trăm). Cho biết mẫu vật chỉ có nguyên tử \(_{19}^{40}\;{\rm{K}}\) và có số mol \({\rm{n}} = 0,5\;{\rm{mol}},1{\rm{MeV}} = 1,6 \cdot {10^{ - 13}}\;{\rm{J}}\).
Sử dụng các thông tin sau cho Câu 5 và Câu 6: Người ta thường tính toán tuổi của các thiên thạch hay mẫu vật dựa vào độ phóng xạ của nó hay tỉ lệ giữa nó với các nguyên tố được tạo ra. Trong tình huống này ta xem xét một mẫu đá Mặt trăng có tỉ lệ số nguyên tử \(_{18}^{40}{\rm{Ar}}\) (bền) và số nguyên tử \(_{19}^{40}\;{\rm{K}}\) trong mẫu là 10,3. Cho rằng các nguyên tử \(_{18}^{40}{\rm{Ar}}\) được tạo ra bởi sự phóng xạ của \(_{19}^{40}\;{\rm{K}}\), chu kỳ bán rã của \(_{19}^{40}\;{\rm{K}}\) là 1,251 tỉ năm. Biết 1 năm có 365 ngày, 1 ngày 24 giờ.
Phân rã của \(_{19}^{40}\;{\rm{K}}\) là phân rã \({\beta ^ + }\)phát ra tia gamma và một neutrino. Một nguyên tử \(_{19}^{40}\;{\rm{K}}\) phân rã sẽ tỏa ra năng lượng cỡ \({{\rm{E}}_1} = 4,6{\rm{MeV}}\). Tính năng lượng tỏa ra trong 1 s của một mẫu vật tính theo đơn vị \(\mu {\rm{J}}\) (làm tròn kết quả đến chữ số hàng phần trăm). Cho biết mẫu vật chỉ có nguyên tử \(_{19}^{40}\;{\rm{K}}\) và có số mol \({\rm{n}} = 0,5\;{\rm{mol}},1{\rm{MeV}} = 1,6 \cdot {10^{ - 13}}\;{\rm{J}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn
\({N_0} = n{N_A} = 0,5 \cdot 6,02 \cdot {10^{23}} = 3,01 \cdot {10^{23}}\)
\({H_0} = \lambda {N_0} = \frac{{\ln 2}}{T} \cdot {N_0} = \frac{{\ln 2}}{{1,251 \cdot {{10}^9} \cdot 365 \cdot 24 \cdot 60 \cdot 60}} \cdot 3,01 \cdot {10^{23}} \approx 5,29 \cdot {10^6}Bq\)
\(P = {H_0}{E_1} = 5,29 \cdot {10^6} \cdot 4,6 \cdot 1,6 \cdot {10^{ - 13}} \approx 3,89 \cdot {10^{ - 6}}\;{\rm{J}}/{\rm{s}} = 3,89\mu \;{\rm{J}}/{\rm{s}}\)
Đáp án: 3,89
Câu hỏi cùng đoạn
Câu 2:
Mẫu đá Mặt trăng ở trên hình thành cách đây y tỉ năm. Tính y (làm tròn kết quả đến chữ số hàng phần mười).
Mẫu đá Mặt trăng ở trên hình thành cách đây y tỉ năm. Tính y (làm tròn kết quả đến chữ số hàng phần mười).
Lời giải của GV VietJack
Hướng dẫn
\(\frac{{\Delta N}}{N} = \frac{{{N_0}\left( {1 - {2^{\frac{{ - t}}{T}}}} \right)}}{{{N_0} \cdot {2^{\frac{{ - t}}{T}}}}} = {2^{\frac{t}{T}}} - 1 \Rightarrow 10,3 = {2^{\frac{t}{{1,251}}}} - 1 \Rightarrow t \approx 4,4{\rm{ }}\)tỉ năm
Đáp án: 4,4
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn
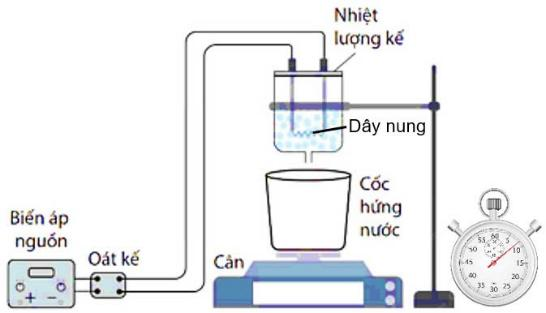
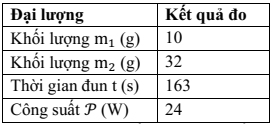
Khối lượng nước đá tan chảy do nhận nhiệt từ nguồn (không tính môi trường) là
\(m = {m_2} - 2{m_1} = 32 - 2 \cdot 10 = 12\;{\rm{g}}\)
\(Q = Pt = 24 \cdot 163 = 3912\;{\rm{J}}\)
\(\lambda = \frac{Q}{m} = \frac{{3912}}{{12 \cdot {{10}^{ - 3}}}} = 326000\;{\rm{J}}/{\rm{kg}}\) Chọn D
Lời giải
a) Đúng. \(_{53}^{131}{\rm{I}} \to _{54}^{131}{\rm{Xe}} + _{ - 1}^0e\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
Đề thi thử tốt nghiệp THPT môn Vật lí Nguyễn Khuyến Lê Thánh Tông - TPHCM có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)