(1,0 điểm) Một chiếc bánh ngọt có dạng hình lăng trụ đứng tam giác có kích thước như hình dưới đây.
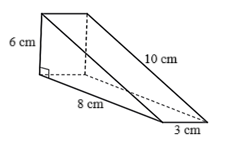
Người ta đặt chiếc bánh ngọt lên một tấm bìa cứng và muốn phủ một lớp kem lên toàn bộ các mặt của chiếc bánh. Biết mỗi cm2 kem cần \(0,25\) gam kem, mỗi gam kem có giá \(500\) đồng. Hỏi phủ kem chiếc bánh như vậy tốn hết bao nhiêu tiền?
Quảng cáo
Trả lời:
Hướng dẫn giải
Diện tích xung quanh của chiếc bánh ngọt đó là: \[\left( {6 + 8 + 10} \right) \cdot 3 = 72\] (cm2).
Diện tích hai đáy của chiếc bánh ngọt đó là: \(2 \cdot \frac{1}{2} \cdot 6 \cdot 8 = 48\) (cm2).
Tổng diện tích cần phủ kem là: \(72 + 48 = 120\) (cm2).
Số gam kem cần để phủ lên bánh là: \(120 \cdot 0,25 = 30\) (gam).
Phủ kem chiếc bánh trên hết số tiền là: \(30 \cdot 500 = 15{\rm{ }}000\) (đồng).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \(\frac{1}{2}A = \frac{1}{{{3^2}}} + \frac{1}{{{5^2}}} + \frac{1}{{{7^2}}} + \frac{1}{{{9^2}}} + ... + \frac{1}{{{{2025}^2}}}\)
Suy ra \(A = \frac{2}{{{3^2}}} + \frac{2}{{{5^2}}} + \frac{2}{{{7^2}}} + \frac{2}{{{9^2}}} + ... + \frac{2}{{{{2025}^2}}}\)
Nhận thấy \(\frac{2}{{{3^2}}} = \frac{2}{9} < \frac{2}{8} = \frac{2}{{2.4}}\)
\(\frac{2}{{{5^2}}} = \frac{2}{{25}} < \frac{2}{{24}} = \frac{2}{{4.6}}\)
…….
\(\frac{2}{{{{2025}^2}}} = \frac{2}{{2025.2025}} < \frac{2}{{2024.2026}}\).
Cộng theo vế, ta được:
\(\frac{2}{{{3^2}}} + \frac{2}{{{5^2}}} + \frac{2}{{{7^2}}} + \frac{2}{{{9^2}}} + ... + \frac{2}{{{{2025}^2}}} < \frac{2}{{2.4}} + \frac{2}{{4.6}} + ... + \frac{2}{{2024.2026}}\)
\(A < \frac{1}{2} - \frac{1}{4} + \frac{1}{4} - \frac{1}{6} + ... + \frac{1}{{2024}} - \frac{1}{{2026}}\)
\(A < \frac{1}{2} - \frac{1}{{2026}}\)
\(A < \frac{{506}}{{1013}}\).
Vậy \(A < \frac{{506}}{{1013}}\).
Lời giải
Hướng dẫn giải
|
a) \(\frac{{31}}{{23}} - \left( {\frac{7}{{32}} + \frac{8}{{23}}} \right)\) \( = \frac{{31}}{{23}} - \frac{7}{{32}} - \frac{8}{{23}}\) \( = \left( {\frac{{31}}{{23}} - \frac{8}{{23}}} \right) - \frac{7}{{32}}\) \( = \frac{{23}}{{23}} - \frac{7}{{32}}\) \( = 1 - \frac{7}{{32}}\) \( = \frac{{25}}{{32}}.\) |
b) \(\left( {1 - \frac{2}{3} - \frac{1}{4}} \right):{\left( {\frac{4}{5} - \frac{3}{4}} \right)^2}\) \( = \left( {\frac{{12}}{{12}} - \frac{8}{{12}} - \frac{3}{{12}}} \right):{\left( {\frac{{16}}{{20}} - \frac{{15}}{{20}}} \right)^2}\) \( = \frac{1}{{12}}:{\left( {\frac{1}{{20}}} \right)^2}\) \( = \frac{1}{{12}}:\frac{1}{{400}}\) \( = \frac{1}{{12}}.400\) \( = \frac{{400}}{{12}}\) \( = \frac{{100}}{3}.\) |
c) \({\left( { - \frac{1}{2}} \right)^2}.\frac{2}{3} + \sqrt {81} .\left( {\frac{{ - 2}}{3}} \right) + 1\frac{1}{2}.\sqrt {\frac{4}{9}} \) \( = \frac{1}{4}.\frac{2}{3} - \sqrt {{9^2}} .\frac{2}{3} + \frac{3}{2}.\sqrt {{{\left( {\frac{2}{3}} \right)}^2}} \) \( = \frac{1}{4}.\frac{2}{3} - 9.\frac{2}{3} + \frac{3}{2}.\frac{2}{3}\) \( = \left( {\frac{1}{4} - 9 + \frac{3}{2}} \right).\frac{2}{3}\) \( = \left( {\frac{1}{4} - \frac{{36}}{4} + \frac{6}{4}} \right).\frac{2}{3}\) \( = - \frac{{29}}{4}.\frac{2}{3}\) \( = - \frac{{29}}{6}\). |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
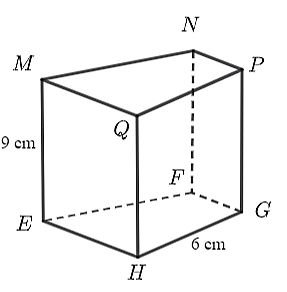
A. \(PG = 9{\rm{ cm}}{\rm{.}}\)
B. \(EH = 9{\rm{ cm}}{\rm{.}}\)
C. \(PQ = 6{\rm{ cm}}{\rm{.}}\)
D. Mặt đáy của lăng trụ đứng là tứ giác \(MNPQ.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.