Cho hình lăng trụ đứng \(ABC.A'B'C'\) có kích thước như hình vẽ dưới đây.
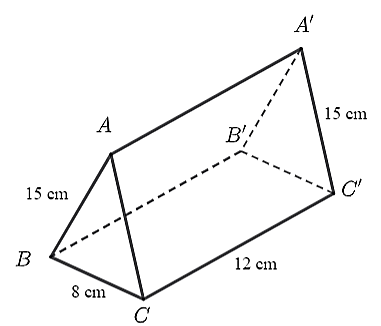
a) Mặt đáy của hình lăng trụ \(ABC.A'B'C'\) là \(BCC'B'.\)
b) \(AC = A'C' = 15{\rm{ cm}}{\rm{.}}\)
c) Chu vi đáy của hình lăng trụ \(ABC.A'B'C'\) là \(40{\rm{ cm}}{\rm{.}}\)
d) Diện tích xung quanh của hình lăng trụ \(ABC.A'B'C'\) lớn hơn \(450{\rm{ c}}{{\rm{m}}^2}.\)
Câu hỏi trong đề: Bộ 2 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: a) Sai.b) Đúng.c) Sai.d) Đúng.
• Nhận thấy đáy của hình lăng trụ \(ABC.A'B'C'\) là \(ABC\) và \(A'B'C'\). Do đó, ý a) là sai.
• Vì hình lăng trụ đứng có hai mặt đáy song song và bằng nhau nên \(AC = A'C' = 15{\rm{ cm}}{\rm{.}}\) Do đó, ý b) là đúng.
• Chu vi đáy của hình lăng trụ đó là: \(15 + 15 + 8 = 38{\rm{ (cm)}}\). Do đó, ý c) là sai.
• Diện tích xung quanh của hình lăng trụ đứng tam giác đó là: \[38.12 = 456\] (cm2).
Do đó, ý d) là đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
|
a) \(\frac{7}{5} + \frac{5}{7}.\left( { - \frac{7}{{25}}} \right)\) \( = \frac{7}{5} + \left( { - \frac{1}{5}} \right)\) \( = \frac{6}{5}\). |
b) \({\left( {\frac{2}{3}} \right)^3} - 4.{\left( { - 1\frac{3}{4}} \right)^2} + {\left( { - \frac{2}{3}} \right)^3}\) \( = \frac{8}{{27}} - 4.{\left( { - \frac{7}{4}} \right)^2} + \left( { - \frac{8}{{27}}} \right)\) \( = \frac{8}{{27}} - 4.\frac{{49}}{{16}} - \frac{8}{{27}}\) \( = \left( {\frac{8}{{27}} - \frac{8}{{27}}} \right) - \frac{{49}}{4}\) \( = 0 - \frac{{49}}{4}\) \( = - \frac{{49}}{4}.\) |
c) \({\left( {\frac{5}{7}} \right)^2}:\left( { - \frac{3}{5}} \right) - \frac{{24}}{{49}}:\sqrt {\frac{9}{{25}}} \) \( = \frac{{25}}{{49}}:\frac{3}{{ - 5}} - \frac{{24}}{{49}}:\sqrt {{{\left( {\frac{3}{5}} \right)}^2}} \) \( = \frac{{25}}{{49}} \cdot \frac{{ - 5}}{3} - \frac{{24}}{{49}}:\frac{3}{5}\) \( = - \frac{{25}}{{49}} \cdot \frac{5}{3} - \frac{{24}}{{49}} \cdot \frac{5}{3}\) \( = \frac{5}{3} \cdot \left( { - \frac{{25}}{{49}} - \frac{{24}}{{49}}} \right)\) \( = \frac{5}{3} \cdot \frac{{ - 49}}{{49}}\) \( = \frac{5}{3} \cdot \left( { - 1} \right)\)\( = - \frac{5}{3}.\) |
Lời giải
Hướng dẫn giải
Đáp án: \(40\).
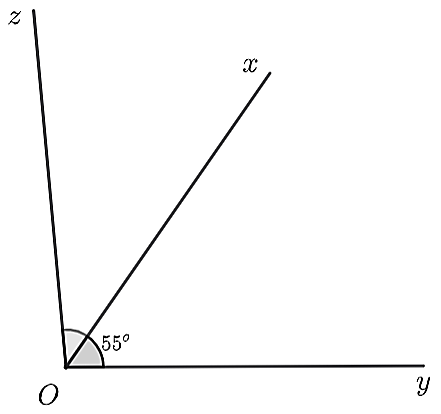
Vì tia \(Ox\) nằm giữa hai tia \(Oy,Oz\) nên ta có \(\widehat {xOy}\) và \(\widehat {xOz}\) là hai góc kề nhau.
Do đó, ta có \(\widehat {xOy} + \widehat {xOz} = \widehat {yOz}\) hay \(55^\circ + \widehat {xOz} = 95^\circ \), suy ra \(\widehat {xOz} = 95^\circ - 55^\circ = 40^\circ \).
Vậy \(\widehat {xOz} = 40^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(AC.\)
B. \(MD.\)
C. \(BQ.\)
D. \(PM.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.