Trong các số sau: \[0;\,\,\pi ;\,\,\frac{{41}}{{11}};\,\,\sqrt {25} ;\,\,\sqrt {3\frac{8}{{11}}} ;\,\, - 2;\,\,\sqrt {0,001} ;\,\,15,21;\,\,7 + \sqrt 4 \], có bao nhiêu số là số vô tỉ?
Câu hỏi trong đề: Bộ 2 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: \(3\).
Ta có:
• Số 0 không là số vô tỉ.
• Số \(\pi \) là một số vô tỉ.
• \(\frac{{41}}{{11}}\) là một số hữu tỉ.
• \(\sqrt {25} = \sqrt {{5^2}} = 5\) là một số hữu tỉ.
• \(\sqrt {3\frac{8}{{11}}} = \sqrt {\frac{{41}}{{11}}} = 1,930614598.....\). là một số vô tỉ.
• \(\sqrt {0,001} = 0,0316227766.....\) là một số vô tỉ.
• \( - 2\) là một số hữu tỉ.
• \(15,21\) là số hữu tỉ.
• \(7 + \sqrt 4 = 7 + 2 = 9\) là một số hữu tỉ.
Do đó, các số vô tỉ là \[\pi ;\,\,\sqrt {3\frac{8}{{11}}} ;\,\,\sqrt {0,001} \]. Vậy có 3 số vô tỉ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng.b) Đúng. c) Sai.d) Sai.
⦁ Sau một giờ, người thứ hai đi được \(1:3 = \frac{1}{3}\) (quãng đường). Do đó ý a) là đúng.
⦁ Sau một giờ, người thứ nhất đi được \(1:6 = \frac{1}{6}\) (quãng đường). Do đó ý b) là đúng.
⦁ Vì người thứ hai khởi hành sau người thứ nhất hai giờ nên khi người thứ hai đi được 1 giờ thì người thứ nhất đã đi được 3 giờ.
Do đó, người thứ nhất đã đi được \(3.\frac{1}{6} = \frac{1}{2}\) (quãng đường).
Suy ra tổng quãng đường hai người đó đã đi được là: \(\frac{1}{3} + \frac{1}{2} = \frac{5}{6}\) (quãng đường). Do đó ý c) là sai.
⦁ Nhận thấy \(\frac{5}{6} < 1\) nên hai người chưa gặp nhau. Do đó ý d) là sai.
Lời giải
Hướng dẫn giải
Đáp án: \(150\).
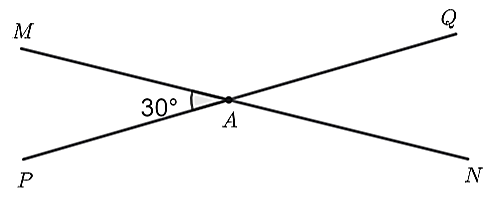
Vì đường thẳng \(MN\) và \(PQ\) cắt nhau tại \(A\) nên \(\widehat {MAP}\) và \(\widehat {MAQ}\) là hai góc kề bù.
Do đó, ta có: \(\widehat {MAQ} + \widehat {MAP} = 180^\circ \) hay \(\widehat {MAQ} + 30^\circ = 180^\circ \).
Suy ra \(\widehat {MAQ} = 180^\circ - 30^\circ = 150^\circ .\)
Vậy \(\widehat {MAQ} = 150^\circ .\)
Câu 3
A. \(\frac{{6,5}}{{14}}.\)
B. \(\frac{3}{7}.\)
C. \(\frac{{21}}{0}.\)
D. \(\frac{{15}}{{0,2}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.