3.1 Trong hộp có \(7\) bút xanh và \(3\) bút đỏ. Lấy ngẫu nhiên \(1\) bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên \(50\) lần thì có \(20\) lần lấy được bút màu xanh. Tính xác suất thực nghiệm của sự kiến “Lấy được bút màu đỏ”.
3.2. Cho \(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\). Chứng minh rằng \(\frac{1}{5} < M < \frac{2}{5}.\)
3.1 Trong hộp có \(7\) bút xanh và \(3\) bút đỏ. Lấy ngẫu nhiên \(1\) bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên \(50\) lần thì có \(20\) lần lấy được bút màu xanh. Tính xác suất thực nghiệm của sự kiến “Lấy được bút màu đỏ”.
3.2. Cho \(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\). Chứng minh rằng \(\frac{1}{5} < M < \frac{2}{5}.\)
Quảng cáo
Trả lời:
3.1. Số lần lấy một chiếc bút là: \(n = 50.\)
Số lần lấy được bút màu đỏ là: \(k = 50 - 20 = 30\) (lần)
Xác suất thực nghiệm của sự kiện “lấy được bút màu đỏ” là: \(\frac{k}{n} = \frac{{30}}{{50}} = \frac{3}{5}.\)
3.2. Ta có:
\(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\)
\(M = \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5}} \right) + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right)\)
\(M = \frac{{13}}{{60}} + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right)\)
Nhận thấy \(\frac{{13}}{{60}} > \frac{{12}}{{60}}\)
Do đó, \(\frac{{13}}{{60}} + \left( {\frac{1}{6} - \frac{1}{7}} \right) + \left( {\frac{1}{8} - \frac{1}{9}} \right) + ... + \left( {\frac{1}{{2022}} - \frac{1}{{2023}}} \right) > \frac{{12}}{{60}}\) hay \(M > \frac{{12}}{{60}}\).
Suy ra \(M > \frac{1}{5}\) (1).
Lại có: \(M = \frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6} - \frac{1}{7} + \frac{1}{8} - \frac{1}{9} + ... + \frac{1}{{2022}} - \frac{1}{{2023}}\)
\(M = \left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{4} - \frac{1}{5} + \frac{1}{6}} \right) - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}}\)
\(M = \frac{{23}}{{60}} - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}}\)
Nhận thấy \(\frac{{23}}{{60}} < \frac{{24}}{{60}}\).
Suy ra \(\frac{{23}}{{60}} - \left( {\frac{1}{7} - \frac{1}{8}} \right) - \left( {\frac{1}{9} - \frac{1}{{10}}} \right) - ... - \left( {\frac{1}{{2021}} - \frac{1}{{2022}}} \right) - \frac{1}{{2023}} < \frac{{24}}{{60}}\).
Do đó, \(M < \frac{{24}}{{60}}\) hay \(M < \frac{2}{5}\) (2)
Từ (1) và (2) ta có \(\frac{1}{5} < M < \frac{2}{5}\) (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có hình vẽ:
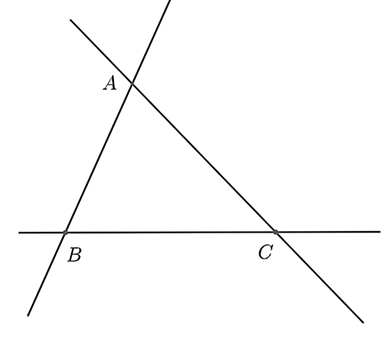
• Các đường thẳng kẻ được là \(AB,AC,BC.\)
• Giao điểm của từng cặp đường thẳng như sau:
- Hai đường thẳng \(AB,AC\) cắt nhau tại \(A\).
- Hai đường thẳng \(AB,BC\) cắt nhau tại \(B.\)
- Hai đường thẳng \(AC,BC\) cắt nhau tại \(C.\)
b)
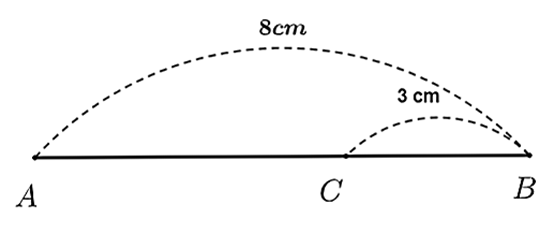
Vì điểm \(C\) nằm giữa hai điểm \(A\) và \(B\) nên ta có \(AC + BC = AB\),
do đó \(AC = AB - CB = 8 - 3 = 5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Vì \(5{\rm{ cm}} > 3{\rm{ cm}}\) nên \(AC > BC.\)
Vậy \(AC > BC.\)
Lời giải
Đáp án: \(35\)
Số viên bi màu trắng là: \(50 - 20 - 18 = 12\) (viên).
Nhận thấy, trường hợp kém may mắn nhất là: lấy ra được \(20\) viên bi đỏ, \(12\) viên bi màu trắng và \(2\) viên bi màu xanh. Sau đó, lấy thêm một viên nữa, là màu xanh.
Do đó, cần lấy ra ngẫu nhiên ít nhất số lần là: \(20 + 12 + 2 + 1 = 35\) (viên bi).
Vậy cần lấy ngẫu nhiên ít nhất \(35\) lần để lấy được \(3\) viên bi màu xanh.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
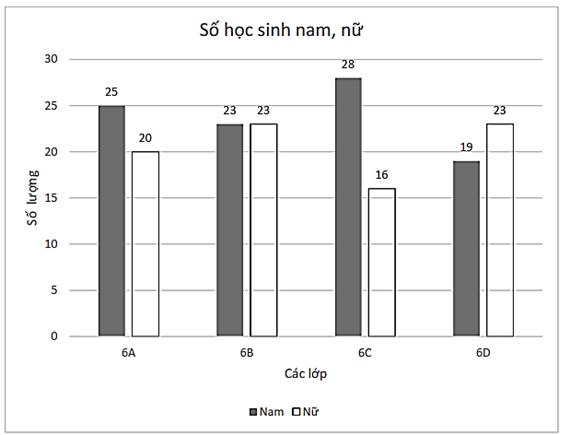
Câu 5
A. Lớp 6A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
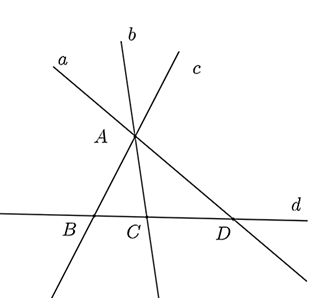 a) Điểm \(A\) thuộc các đường thẳng \(a,b,c\).
a) Điểm \(A\) thuộc các đường thẳng \(a,b,c\).