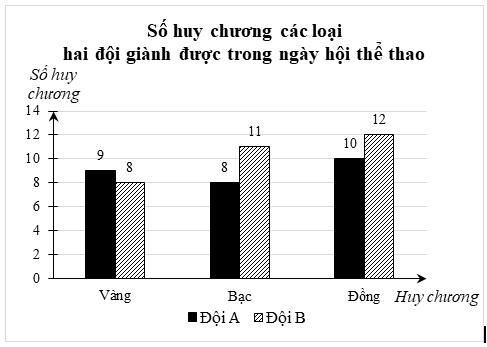
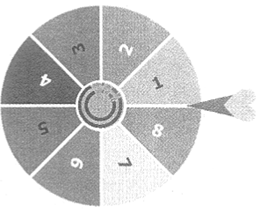
Thực hiện phép tính (tính hợp lí nếu có thể):

a) \[\frac{7}{{30}} + \frac{{ - 12}}{{37}} + \frac{{23}}{{30}} + \frac{{ - 25}}{{37}}.\]        

b) \(\left( { - 0,4} \right) \cdot \left( { - 0,5} \right) \cdot \left( { - 0,8} \right).\)

c) \(\frac{2}{{11}} \cdot \frac{{ - 5}}{4} + \frac{{ - 9}}{{11}} \cdot \frac{5}{4} + 1\frac{3}{4}.\)           

d) \(\left( {\frac{5}{7} \cdot 0,6 - 5:3\frac{1}{2}} \right) \cdot \left( {40\% - 1,4} \right) \cdot {\left( { - \frac{2}{3}} \right)^3}.\)

1) a) Biểu đồ cột kép trên cho biết về số huy chương các loại (Vàng, Bạc, Đồng) mà đội A và đội B giành được trong ngày hội thể thao.

b) Tổng số huy chương các loại của đội A là: \(9 + 8 + 10 = 27\) (huy chương).

Tổng số huy chương các loại của đội B là: \(8 + 11 + 12 = 31\) (huy chương).

c) Tổng số điểm đội A đạt được là: \(9 \cdot 5 + 8 \cdot 4 + 10 \cdot 3 = 107\) (điểm).

Tổng số điểm đội B đạt được là: \(8 \cdot 5 + 11 \cdot 4 + 12 \cdot 3 = 120\) (điểm).

Như vậy, đội B đạt được tổng số điểm nhiều hơn, và nhiều hơn \(120 - 107 = 13\) điểm.

2) Trong 30 lượt quay, ta thấy có các kết quả mũi tên chỉ số chẵn là:

\(8,\,\,8,\,\,4,\,\,6,\,\,6,\,\,6,\,\,6,\,\,4,\,\,8,\,\,6,\,\,8,\,\,4,\,\,6,\,\,8.\)

Như vậy, có tất cả 14 lượt quay mũi tên chỉ vào số chẵn.

Vậy xác suất thực nghiệm của sự kiện “An thắng” là: \(\frac{{14}}{{30}} = \frac{7}{{15}}.\)

Xét hai lớp cuối cùng là lớp thứ \(n - 1\) và lớp thứ \(n.\)

Lớp thứ \(n - 1\) được chia \(x\) cây và \(\frac{1}{8}\) số cây còn lại, hay \(x + \frac{1}{8}y\) (cây) (với \(y\) là số cây còn lại sau lớp thứ \(n - 2\) trồng).

Lớp thứ \(n\) là lớp cuối cùng được chia nốt \(y - \frac{1}{8}y = \frac{7}{8}y\) (cây), số cây này nếu theo đúng quy luật của bài toán thì bằng \(x + 5\) (cây) (do không còn số còn lại).

Vì số cây các lớp được chia đem trồng đều bằng nhau nên ta có: \(x + \frac{1}{8}y = x + 5,\) hay \(\frac{1}{8}y = 5,\) suy ra \(y = 40\) (cây).

Khi đó, lớp cuối cùng được chia nốt số cây là: \(\frac{7}{8} \cdot 40 = 35\) (cây), cũng tức là mỗi lớp được chia 35 cây.

Vì lớp 6A trồng 10 cây và \(\frac{1}{8}\) số cây còn lại nên \(\frac{1}{8}\) số cây còn lại chính bằng \(35 - 10 = 25\) (cây).

Tổng số cây là: \(10 + 25:\frac{1}{8} = 210\) (cây).

Số lớp 6 là: \(210:35 = 6\) (lớp).

Vậy có 6 lớp 6 và mỗi lớp được chia 35 cây đem trồng.