Trong một thùng đựng \(20\) quả bóng được đánh số \(5;6;7;....;23;24\). Lấy ngẫu nhiên một quả bóng.

     a) Viết tập hợp \(M\) gồm các kết quả có thể xảy ra đối với số xuất hiện trên quả bóng được rút ra.

     b) Tính xác suất của biến cố \(N\): “Quả bóng lấy ra là số lẻ”.

     c) Tính xác suất của biến cố \(P\) : “Quả bóng lấy ra là ước của \(48\)”.

2.1. Thay \(x =  - 1,y = 3\) vào biểu thức \(B = 3{x^2}y + 6{x^2}{y^2} + 3x{y^2}\), ta được:

            \(B = 3.{\left( { - 1} \right)^2}.3 + 6{\left( { - 1} \right)^2}{.3^2} + 3.\left( { - 1} \right){.3^2} = 36\).

 Vậy giá trị của biểu thức \(B = 36\).

2.2. a) \(A\left( x \right) =  - \frac{5}{3}{x^2} + \frac{3}{4}{x^4} + 2x - \frac{7}{3}{x^2} - 3 + 4x + \frac{1}{4}{x^4}\)

             \( = \left( {\frac{3}{4} + \frac{1}{4}} \right){x^4} + \left( { - \frac{5}{3} - \frac{7}{3}} \right){x^2} + \left( {2 + 4} \right)x - 3\)

              \( = {x^4} - 4{x^2} + 6x - 3\).

b) Đa thức \(A\left( x \right)\) có bậc 4 và hệ số cao nhất là 1.

c) \(B\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 2} \right)\)

            \( = {x^4} - 2{x^2} - {x^2} + 2\)

            \( = {x^4} - 3{x^2} + 2\).

Ta có \(A\left( x \right) + C\left( x \right) = B\left( x \right)\)

Suy ra \(C\left( x \right) = B\left( x \right) - A\left( x \right)\)

                     \( = {x^4} - 3{x^2} + 2 - \left( {{x^4} - 4{x^2} + 6x - 3} \right)\)

                     \( = {x^4} - 3{x^2} + 2 - {x^4} + 4{x^2} - 6x + 3\)

                     \( = {x^2} - 6x + 5\).

d) Ta có:

• \(B\left( { - 1} \right) = {\left( { - 1} \right)^4} - 3.{\left( { - 1} \right)^2} + 2 = 1 - 3 + 2 = 0\).

Do đó \(x =  - 1\) là nghiệm của đa thức \(B\left( x \right)\).

• \(C\left( { - 1} \right) = {\left( { - 1} \right)^2} - 6.\left( { - 1} \right) + 5 = 1 + 6 + 5 = 12\).

Do đó \(x =  - 1\) không là nghiệm của đa thức \(C\left( x \right)\).

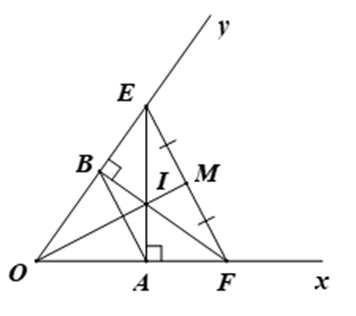
a) Xét \(\Delta OAE\) và \(\Delta OBF\), có:

\(\widehat {OAE} = \widehat {OBF} = 90^\circ \)

\(OA = OB\) (giả thiết)

\(\widehat {AOB}\) là góc chung

Do đó, \(\Delta OAE = \Delta OBF\) (cgv – gn)

Suy ra \(OE = OF\) (hai cạnh tương ứng)

b) Áp dụng bất đẳng thức tam giác cho \(\Delta EIF\), ta được: \(EF < EI + IF\).

Mà \(2EM = EF\) (do \(M\) là trung điểm của \(EF\))

Suy ra \(2EM < EI + IF.\)

Vậy \(EM < \frac{{EI + IF}}{2}.\)

c) Xét \(\Delta EOF\) có hai đường cao \(FB\) và \(AE\) cắt nhau tại \(I\).

Suy ra \(I\) là trực tâm của \(\Delta OEF.\)

Do đó, \(OI \bot EF\) (1)

Xét \(\Delta OEM\) và \(\Delta OFM\), có:

\(OM\) là cạnh chung

\(ME = MF\) (do \(M\) là trung điểm của \(EF\))

\(OE = OF\) (câu a)

Do đó, \(\Delta OEM = \Delta OFM\) (c.c.c)

Suy ra \(\widehat {OME} = \widehat {OMF}\) (hai góc tương ứng)

Mà \(\widehat {OME} + \widehat {OMF} = 180^\circ \) (hai góc kề bù)

Do đó, \(\widehat {OME} = \widehat {OMF} = 90^\circ \) hay \(OM \bot EF\) (2)

Từ (1) và (2) suy ra \(O,I,M\) thẳng hàng.