(1,5 điểm) Cho \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch. Ta có bảng sau:
a) Xác định hệ số tỉ lệ của \(y\) đối với \(x\).
b) Điền số thích hợp để hoàn thiện bảng trên.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Vì \(x\) và \(y\) là hai đại lượng tỉ lệ nghịch và từ bảng trên có \(x = - 2\) thì \(y = - 15\).
Từ đây, ta có: \(a = xy = - 2.\left( { - 15} \right) = 30\). Suy ra \(y = \frac{{30}}{x}\).
Do đó, hệ số tỉ lệ của \(y\) đối với \(x\) là \(30\).
b) Ta có \(a = 30\) nên ta được bảng sau:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
a) \(\frac{x}{3} = \frac{{2,5}}{{1,5}}\) suy ra \(1,5x = 2,5.3\), do đó \(x = \frac{{2,5.3}}{{1,5}} = 5\).
Vậy \(x = 5\).
b) \(\frac{x}{{15}} = \frac{y}{7}\) và \(y - x = 16\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{15}} = \frac{y}{7} = \frac{{y - x}}{{7 - 15}} = \frac{{16}}{{ - 8}} = - 2\).
Suy ra \(x = 15.\left( { - 2} \right) = - 30\) và \(y = 7.\left( { - 2} \right) = - 14\).
Vậy \(x = - 30\) và \(y = - 14\).
c) \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) và \(x - 2y + 3z = 38.\)
Ta có \(\frac{x}{2} = \frac{y}{3} = \frac{z}{5}\) hay \(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}}\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2} = \frac{{2y}}{6} = \frac{{3z}}{{15}} = \frac{{x - 2y + 3z}}{{2 + 6 + 15}} = \frac{{38}}{{23}}\).
Suy ra \(x = \frac{{76}}{{23}};y = \frac{{119}}{{23}};z = \frac{{190}}{{23}}\).
Lời giải
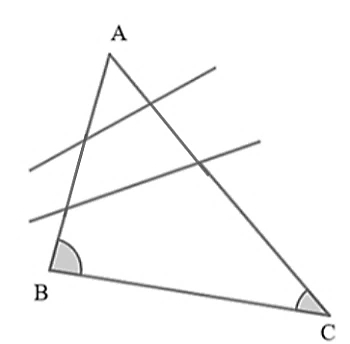
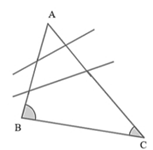
4.1. Từ hình minh họa, xét tam giác \(ABC\), có \(\widehat B > \widehat C{\rm{ }}\left( {75^\circ > 35^\circ } \right)\) nên \(AC > AB\) (quan hệ giữa góc và cạnh đối diện trong tam giác).
Do đó, bạn Đào đi đến nhà bạn Lan ngắn hơn quãng đường bạn Đào đi đến nhà bạn Hồng.
Vậy các bạn nên học nhóm ở nhà bạn Lan.
4.2. a) Xét \(\Delta AMB\) và \(\Delta AMC\), có:
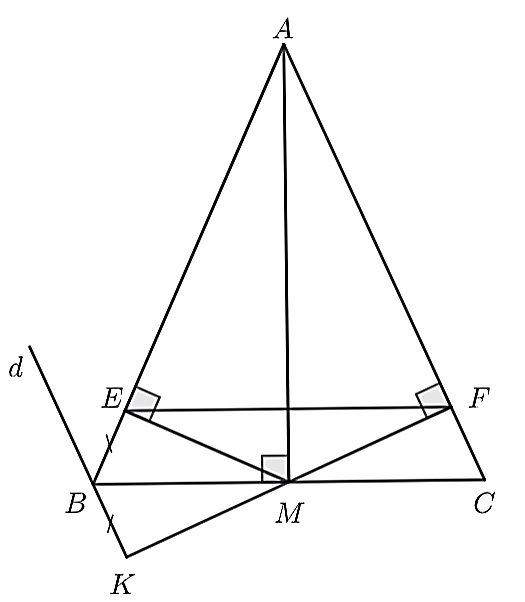
\(AM\) chung (gt)
\(BM = MC\) (gt)
\(AB = AC\) (\(\Delta ABC\) cân)
Do đó, \(\Delta AMB = \Delta AMC\) (c.c.c)
Suy ra \(\widehat {MAB} = \widehat {MAC}\) (hai cạnh tương ứng)
Do đó, \(AM\) là tia phân giác của \(\widehat {BAC}\).
b) Xét \(\Delta AME\) và \(\Delta AMF\), có:
\(\widehat {MEA} = \widehat {MFA} = 90^\circ \) (gt)
\(\widehat {EAM} = \widehat {FAM}\)
\(AM\) chung (gt)
Do đó, \(\Delta AME = \Delta AMF\) (ch – gn)
Suy ra \(ME = MF\) (hai cạnh tương ứng)
Từ đó, ta có: \(\Delta MEF\) cân tại \(M\).
c) Vì \(\Delta AME = \Delta AMF\) (cmt) nên \(AE = AF\) (hai cạnh tương ứng).
Mà \(AB = AC\) và ta có: \(\left\{ \begin{array}{l}AB = AE + EB\\AC = AF + FC\end{array} \right.\) suy ra \(EB = FC\).
Lại có \(EB = KB\) nên \(KB = FC\).
Xét \(\Delta BKM\) và \(\Delta CFM\), có:
\(BM = MC\) (gt)
\(\widehat {FCM} = \widehat {MBK}\) (so le trong)
\(KB = FC\) (cmt)
Do đó, \(\Delta BKM = \Delta CFM\) (c.g.c)
Suy ra \(\widehat {BMK} = \widehat {CMF}\) (hai góc tương ứng)
Mà hai góc ở vị trí đối đỉnh nên \(K,M,F\) thẳng hàng.
Lại có \(KM = MF\) (hai cạnh tương ứng)
Do đó, \(M\) là trung điểm của \(KF\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo