(4,0 điểm)

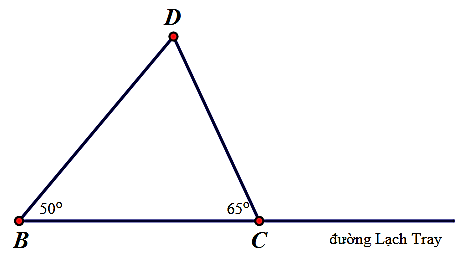
4.1. Bạn Hòa đi học từ nhà đến trường bằng cách đi xe buýt dọc theo tuyến đường Lạch Tray và xuống xe tại một trong hai điểm dừng \(B\) hoặc \(C\), rồi từ đó đi bộ đến trường tại vị trí điểm \(D\). Bạn Hòa nên xuống đi bộ ở điểm dừng nào để quãng đường đi bộ đến trường ngắn hơn? Biết \(\widehat B = 50^\circ ,\widehat C = 65^\circ \).

4.2.Cho \(\Delta ABC\) cân tại \(A\). Từ \(A\) kẻ \(AH \bot BC\) tại \(H.\) Chứng minh rằng:

a) \(AH\) là đường trung tuyến của \(\Delta ABC\).

b) Kẻ \(BM \bot AC{\rm{ }}\left( {M \in AC} \right)\). Hãy so sánh \(BM\) với \(BC\) và \(BM\) với \(AC.\)

c) Kẻ \(CK \bot AB{\rm{ }}\left( {K \in AB} \right),\) \(AH\) cắt \(BM\) tại \(I\). Chứng minh \(K,I,C\) thẳng hàng.

Hướng dẫn giải

4.1. Xét \(\Delta DBC\), có \(\widehat B < \widehat C{\rm{ }}\left( {50^\circ < 65^\circ } \right)\).

Do đó, \(BD > DC\) (quan hệ giữa góc và cạnh trong tam giác)

Vậy bạn Hòa nên xuống đi bộ ở điểm dừng \(B\) để quãng đường đi bộ đến trường là ngắn nhất.

4.2. a) Ta có \(\Delta ABC\) cân tại \(A\) và \(AH \bot BC\) tại \(H\) nên \(AH\) vừa là đường cao, vừa là đường trung tuyến của \(\Delta ABC\).

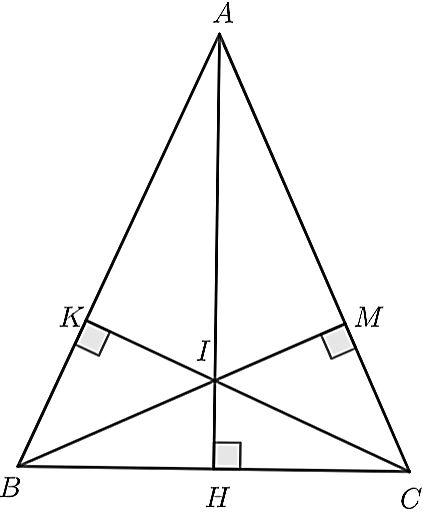
b) Ta có \(BM \bot AC{\rm{ }}\left( {M \in AC} \right)\) nên \(\Delta BMC\) vuông tại \(M\), có \(BC\) là cạnh huyền.

Do đó, \(BM < BC\) (quan hệ giữa các cạnh trong tam giác)

Xét \(\Delta BMA\) vuông tại \(M\) có \(AB\) là cạnh huyền.

Do đó, \(BM < AB\) (1)

Lại có, tam giác \(ABC\) cân tại \(A\) nên \(AB = AC\) (2)

Từ (1) và (2) suy ra \(MB < AC\).

c) Xét \(\Delta KBC\) và \(\Delta MCB\) có:

\(BC\): chung (gt)

\(\widehat {ABC} = \widehat {ACB}\) (tam giác \(ABC\) cân)

\(\widehat {BKC} = \widehat {BMC} = 90^\circ \) (gt)

Suy ra \(\Delta KBC = \Delta MCB\) (ch – gn)

Suy ra \(KB = MC\) (hai cạnh tương ứng).

Lại có: \(\left\{ \begin{array}{l}AB = AK + KB\\AC = AM + MC\end{array} \right.\). Mà \(KB = MC\) (cmt)

Suy ra \(AK = AM\).

Xét \(\Delta KAI\) và \(\Delta MAI\), có:

\(AI\) chung (gt)

\(AK = AM\) (cmt)

\(\widehat {AKI} = \widehat {AMI} = 90^\circ \) (gt)

Suy ra \(\Delta KAI = \Delta MAI\) (ch – cgv)

Suy ra \(KI = MI\) (hai cạnh tương ứng)

Xét \(\Delta KIB\) và \(\Delta MIC\) có:

\(\widehat {IKB} = \widehat {IMC} = 90^\circ \)

\(IK = IM\) (cmt)

\(KB = MC\) (cmt)

Suy ra \(\Delta KIB = \Delta MIC\) (2cgv)

Suy ra \(\widehat {KIB} = \widehat {MIC}\) (hai góc tương ứng)

Mà hai góc ở vị trí đối đỉnh.

Suy ra \(K,I,C\) thẳng hàng.