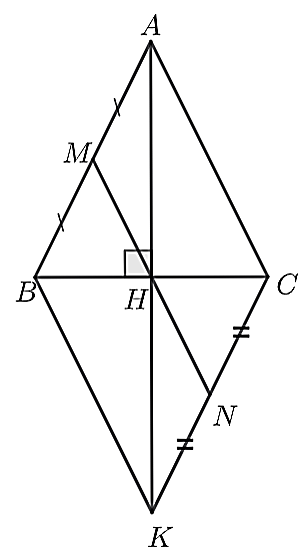
(3,0 điểm) Cho \(\Delta ABC\) cân tại \(A\), gọi \(H\) là trung điểm của \(BC\).
a) Chứng minh \(\Delta ABH = \Delta ACH.\)
b) Trên tia đối của tia \(HA\) lấy điểm \(K\) sao cho \(AH = HK.\) Chứng minh rằng \(AC\parallel BK.\)
c) Gọi \(M,N\) lần lượt là trung điểm của \(AB,CK.\) Chứng minh rằng ba điểm \(M,H,N\) thẳng hàng.
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 7 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a)
Xét \(\Delta ABH\) và \(\Delta ACH\), có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(AH\): chung (gt)
\(\widehat {AHB} = \widehat {AHC} = 90^\circ \) (gt)
Do đó, \(\Delta ABH = \Delta ACH\) (ch – gn).
b) Xét \(\Delta BHK\) và \(\Delta CHA\), có:
\(BH = HC\) (gt)
\(\widehat {BHK} = \widehat {CHA} = 90^\circ \) (đối đỉnh)
\(HA = HK\) (gt)
Do đó, \(\Delta BHK = \Delta CHA\) (c.g.c)
Suy ra \(\widehat {KBH} = \widehat {HCA}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong, suy ra \(AC\parallel BK.\)
c) Xét \(\Delta ABH\) và \(\Delta CHK\), có:
\(HB = HC\) (hai cạnh tương ứng)
\(AH = HK\) (gt)
(đối đỉnh)
Do đó, \(\Delta ABH = \Delta CHK\) (c.g.c)
Suy ra \(\widehat {BAH} = \widehat {HKC}\) (hai góc tương ứng)
Mà hai góc ở vị trí so le trong nên \(AB\parallel KC\).
Lại có \(AB = KC\) (hai cạnh tương ứng).
Mà \(M,N\) là trung điểm của \(AB,CK\). Do đó, \(AM = KN\)
Xét \(\Delta MAH\) và \(\Delta NKH\), có:
\(AM = KN\) (cmt)
\(\widehat {BAH} = \widehat {HKC}\) (cmt)
\(AH = HK\) (gt)
Do đó, \(\Delta MAH = \Delta NKH\) (c.g.c)
Suy ra \(\widehat {MHA} = \widehat {NHK}\) (hai góc tương ứng).
Mà hai góc ở vị trí đối đỉnh, do đó \(M,H,N\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
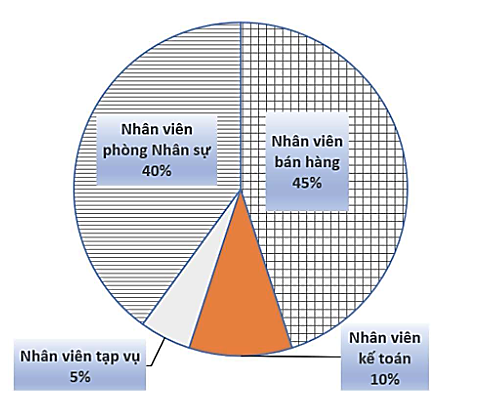
a) Quan sát biểu đồ, ta thấy bộ phận có nhiều nhân viên nhất là bộ phận nhân viên bán hàng (chiếm \(45\% \)).
b) Số nhân viên bộ phận kế toán so với số nhân viên phòng nhân sự là: \(\frac{{10}}{{40}}.100 = 25\% \).
c) Số nhân viên của bộ phận nhân sự là: \(480.40\% = 192\) (nhân viên)
Số nhân viên của bộ phận bán hàng là: \(480.45\% = 214\) (nhân viên)
Số nhân viên của bộ phận tạp vụ là: \(480.5\% = 24\) (nhân viên)
Số nhân viên của bộ phận kế toán là: \(480.10\% = 48\) (nhân viên).
d) Mỗi nhân viên bộ phận kế toán được thưởng số tiền là:
\(10{\rm{ }}800{\rm{ }}000:48 = 225{\rm{ }}000\) (đồng)
Vì mỗi nhân viên được thưởng số tiền như nhau, nên mỗi nhân viên phòng nhân sự cũng được thưởng \({\rm{225 }}000\) đồng.
Do đó, tổng mức thưởng Tết của bộ phận nhân sự là: \(225{\rm{ }}000.192 = 43{\rm{ }}200{\rm{ }}000\) (đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
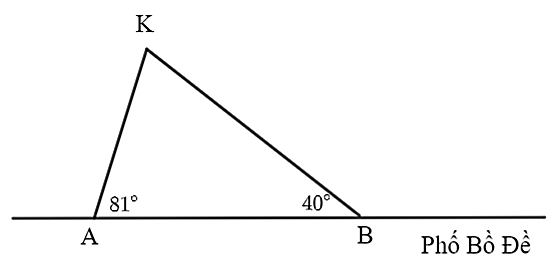
Từ hình vẽ minh họa, xét \(\Delta ABK\), ta có:
\(\widehat A > \widehat B{\rm{ }}\left( {81^\circ > 40^\circ } \right)\), do đó \(KB > KA\) (tính chất của góc và cạnh đối diện trong tam giác).
Vì vậy bạn Cường nên xuống xe ở điểm \(A\) rồi đi bộ đến trường để quãng đường ngắn nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập