(2,5 điểm) Số học sinh đạt điểm giỏi môn Toán trong 4 tháng học kì I của khối lớp 7 được biểu diễn bởi biểu đồ đoạn thẳng sau:

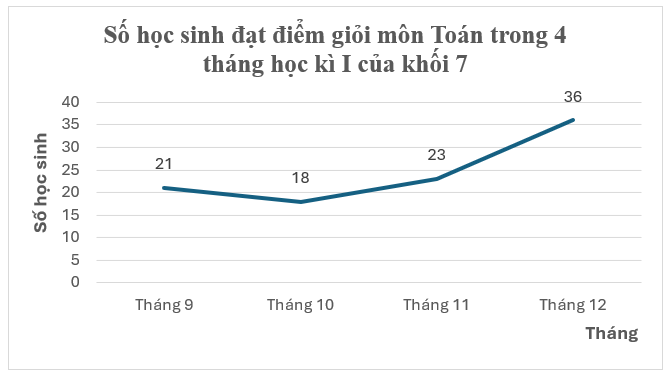
a) Lập bảng dữ liệu theo mẫu sau:

b) Tháng nào có nhiều học sinh đạt điểm giỏi môn Toán của khối 7 nhất? Tháng nào có ít nhất?

c) Từ tháng 11 đến tháng 12, số học sinh đạt điểm giỏi môn Toán của khối lớp 7 tăng bao nhiêu học sinh?

d) Số học sinh đạt điểm giỏi môn Toán tháng 12 tăng bao nhiêu phần trăm so với tháng 10?

Hướng dẫn giải

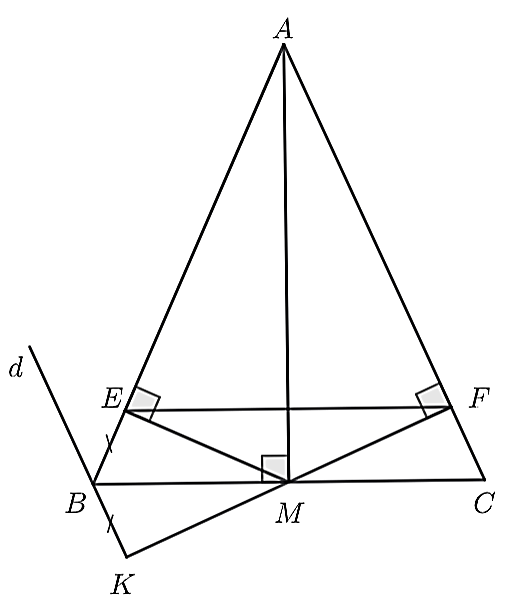
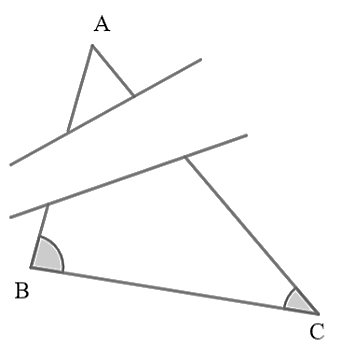
a) Xét

\(\Delta AMB\) và \(\Delta AMC\), có:

\(AM\) chung (gt)

\(BM = MC\) (gt)

\(AB = AC\) (\(\Delta ABC\) cân)

Do đó, \(\Delta AMB = \Delta AMC\) (c.c.c)

Suy ra \(\widehat {MAB} = \widehat {MAC}\) (hai cạnh tương ứng)

Do đó, \(AM\) là tia phân giác của \(\widehat {BAC}\).

b) Xét \(\Delta AME\) và \(\Delta AMF\), có:

\(\widehat {MEA} = \widehat {MFA} = 90^\circ \) (gt)

\(\widehat {EAM} = \widehat {FAM}\)

\(AM\) chung (gt)

Do đó, \(\Delta AME = \Delta AMF\) (ch – gn)

Suy ra \(ME = MF\) (hai cạnh tương ứng)

Từ đó, ta có: \(\Delta MEF\) cân tại \(M\).

c) Vì \(\Delta AME = \Delta AMF\) (cmt) nên \(AE = AF\) (hai cạnh tương ứng).

Mà \(AB = AC\) và ta có: \(\left\{ \begin{array}{l}AB = AE + EB\\AC = AF + FC\end{array} \right.\) suy ra \(EB = FC\).

Lại có \(EB = KB\) nên \(KB = FC\).

Xét \(\Delta BKM\) và \(\Delta CFM\), có:

\(BM = MC\) (gt)

\(\widehat {FCM} = \widehat {MBK}\) (so le trong)

\(KB = FC\) (cmt)

Do đó, \(\Delta BKM = \Delta CFM\) (c.g.c)

Suy ra \(\widehat {BMK} = \widehat {CMF}\) (hai góc tương ứng)

Mà hai góc ở vị trí đối đỉnh nên \(K,M,F\) thẳng hàng.

Lại có \(KM = MF\) (hai cạnh tương ứng)

Do đó, \(M\) là trung điểm của \(KF\).

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: \(A = \left\{ {1;2;3;...;26} \right\}\).

Do đó, có 26 kết quả có thể xảy ra khi rút ngẫu nhiên một thẻ trong hộp.

b) Kết quả thuận lợi của biến cố \(Y\): “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” là:

\(Y = \left\{ {3;6;9;12;15;18;21;24} \right\}\). Do đó, có \(8\) kết quả thuận lợi cho biến cố này.

c) Xác suất của biến cố \(Y:\) “Số ghi trên thẻ được rút ra là số chia hết cho 3” là: \(\frac{8}{{26}} = \frac{4}{{13}}\).

d) Kết quả thuận lợi cho biến cố \(Z\): “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1” là: \(Z = \left\{ {1;21} \right\}\). Do đó, có hai kết quả thuận lợi cho biến cố này.

Vậy xác suất của biến cố \(Z\): “Số xuất hiện trên thẻ được rút ra là số khi chia cho 4 và 5 đều có số dư là 1” là \(\frac{2}{{26}} = \frac{1}{{13}}\).