(3,0 điểm) Cho \(\Delta ABC\) vuông tại \(A\) có \(AB < AC\). Trên cạnh \(BC\) lấy điểm \(D\) sao cho \(BD = BA\). Đường thẳng vuông góc với \(BC\) tại \(D\) cắt cạnh \(AC\) tại \(M\), cắt tia \(BA\) tại \(N.\)
a) Chứng minh \(\Delta ABM = \Delta DBM.\)
b) Chứng minh \(\Delta MNC\) cân.
c) Gọi \(I\) là trung điểm của \(CN\). Chứng minh ba điểm \(B,M,I\) thẳng hàng.
Quảng cáo
Trả lời:
Hướng dẫn giải
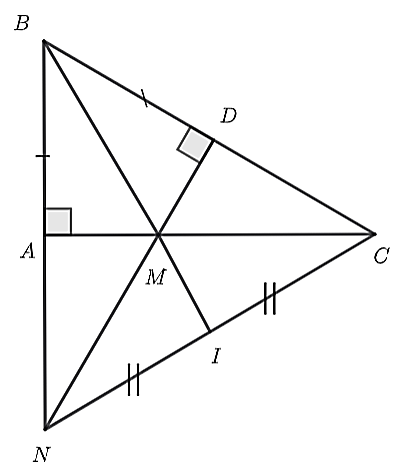
a) Xét tam giác
\(\Delta ABM\) và \(\Delta DBM\), có:
\(AB = BD\) (gt)
\(BM\) chung (gt)
\(\widehat {BAM} = \widehat {MDB} = 90^\circ \) (gt)
Do đó, \(\Delta ABM = \Delta DBM\) (ch – cgv)
b) Do \(\Delta ABM = \Delta DBM\) (cmt) nên \(AM = MD\) (hai cạnh tương ứng)
Xét \(\Delta AMN\) và \(\Delta DMC\), ta có:
\(\widehat {MAN} = \widehat {MDC} = 90^\circ \) (gt)
\(AM = MD\) (cmt)
\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)
Suy ra \(\Delta AMN = \Delta DMC\) (cgv – gn)
Do đó, \(MN = MC\) (hai cạnh tương ứng)
Suy ra \(\Delta MNC\) cân tại \(M.\)
c) Do \(\Delta MNC\) cân tại \(M\) và \(I\) là trung điểm của \(NC\) nên \(MI\) cũng là đường cao của \(\Delta MNC\).
Suy ra \(MI \bot NC\).
Xét \(\Delta AMN\) và \(\Delta DMC,\) có:
\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)
\(AM = MD\) (cmt)
\(MN = MC\) (cmt)
Suy ra \(\Delta AMN = \Delta DMC\) (c.g.c)
Do đó, \(AN = DC\) (hai cạnh tương ứng)
Ta có: \(AB + AN = BN;{\rm{ }}BD + DC = BC\).
Mà \(AN = DC,AB = BD\). Suy ra \(BN = BC\).
Do đó, \(\Delta BNC\) cân tại \(B\).
Suy ra \(BI \bot NC\) tại \(I\).
Mà \(MI \bot NC\) tại \(I\).
Do đó, \(B,M,I\) thẳng hàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
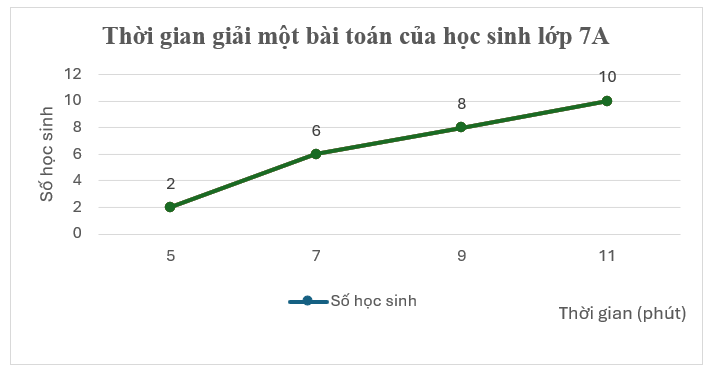
a) Số học sinh làm hết nhiều thời gian nhất là 10 học sinh.
Số học sinh làm hết ít thời gian nhất là 2 học sinh.
Vậy số học sinh làm hết nhiều thời gian nhất hơn số học sinh làm hết ít thời gian nhất là
\(10 - 2 = 8\) (học sinh)

b) Ta có bảng thống kê cho mẫu số liệu ở biểu đồ trên là
c) Số học sinh của lớp 7A là: \(2 + 6 + 8 + 10 = 26\) (học sinh)
d) Số học sinh làm bài nhanh nhất chiếm số phần trăm so với học sinh cả lớp là: \(\frac{2}{{26}}.100 \approx 7,92\% \).
Lời giải
Hướng dẫn giải
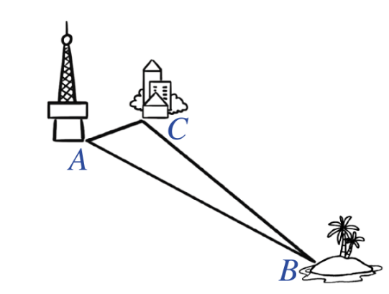
Theo đề và từ hình minh họa, ta có: \(BC = 75{\rm{ km, }}AC = 20{\rm{ km}}\).
Khoảng cách từ trạm phát sóng đến hòn đảo chính là độ dài đoạn \(AB\)
Do đó, áp dụng bất đẳng thức về cạnh trong tam giác \(ABC,\) ta có:
\(BC + AC > AB\) hay \(75 + 20 > AB\) nên \(AB < 95{\rm{ km}}\).
Do đó, sóng \(4G\) của trạm phát sóng tại vị trí \(A\) có thể đến đảo.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.