Bộ 10 đề thi Giữa kì 2 Toán 7 Cánh diều cấu trúc mới có đáp án - Đề 8

Hướng dẫn giải

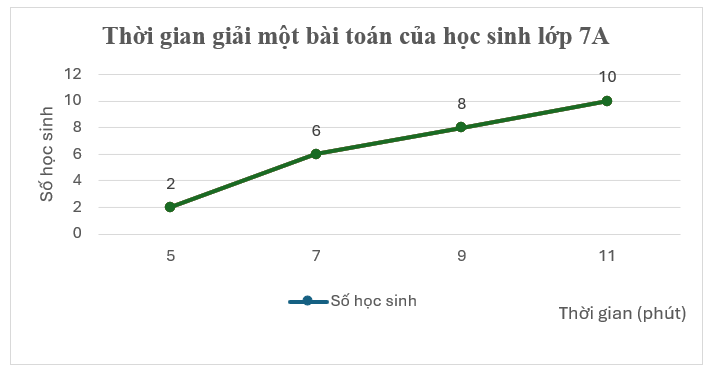
a) Số học sinh làm hết nhiều thời gian nhất là 10 học sinh.

Số học sinh làm hết ít thời gian nhất là 2 học sinh.

Vậy số học sinh làm hết nhiều thời gian nhất hơn số học sinh làm hết ít thời gian nhất là

\(10 - 2 = 8\) (học sinh)

b) Ta có bảng thống kê cho mẫu số liệu ở biểu đồ trên là

c) Số học sinh của lớp 7A là: \(2 + 6 + 8 + 10 = 26\) (học sinh)

d) Số học sinh làm bài nhanh nhất chiếm số phần trăm so với học sinh cả lớp là: \(\frac{2}{{26}}.100 \approx 7,92\% \).

Hướng dẫn giải

a) Tập hợp các kết quả có thể xảy ra khi gieo xúc xắc một lần là: \(A\) = {mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 4 chấm, mặt 5 chấm, mặt 6 chấm}.

b) Các kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số lẻ” là: mặt 1 chấm, mặt 3 chấm, mặt 5 chấm. Do đó, có 3 kết quả thuận lợi cho biến cố trên.

c) Các kết quả thuận lợi cho biến cố: “Mặt xuất hiện của xúc xắc là số nguyên tố” là: mặt 2 chấm, mặt 3 chấm, mặt 5 chấm. Do đó, có 3 kết quả thuận lợi cho biến cố trên.

Do đó, xác suất của biến cố này là: \(\frac{3}{6} = \frac{1}{2}\).

d) Gieo con xúc xắc cân đối đồng chất đó hai lần liên tiếp thì số kết quả có thể xảy ra là:

\(6.6 = 36\) (kết quả)

Các kết quả thuận lợi của biến cố “Tổng số chấm xuất hiện sau hai lần gieo bằng 7” là \(\left( {1;6} \right);\left( {6;1} \right);\)

\(\left( {5;2} \right);\left( {2;5} \right);\left( {3;4} \right);\left( {4;3} \right)\). Do đó, có 6 kết quả thuận lợi.

Vậy xác suất của biến cố trên là: \(\frac{6}{{36}} = \frac{1}{6}\).

Hướng dẫn giải

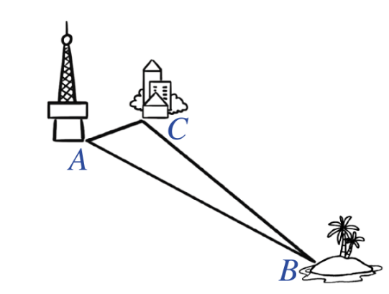
Theo đề và từ hình minh họa, ta có: \(BC = 75{\rm{ km, }}AC = 20{\rm{ km}}\).

Khoảng cách từ trạm phát sóng đến hòn đảo chính là độ dài đoạn \(AB\)

Do đó, áp dụng bất đẳng thức về cạnh trong tam giác \(ABC,\) ta có:

\(BC + AC > AB\) hay \(75 + 20 > AB\) nên \(AB < 95{\rm{ km}}\).

Do đó, sóng \(4G\) của trạm phát sóng tại vị trí \(A\) có thể đến đảo.

Hướng dẫn giải

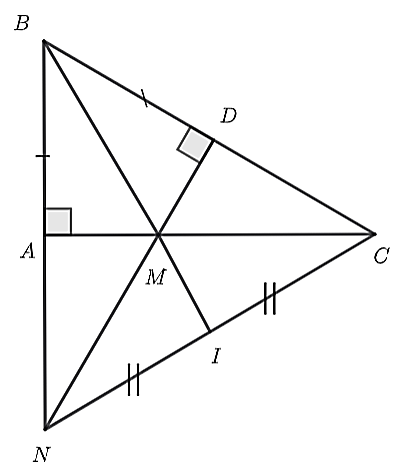
a) Xét tam giác

\(\Delta ABM\) và \(\Delta DBM\), có:

\(AB = BD\) (gt)

\(BM\) chung (gt)

\(\widehat {BAM} = \widehat {MDB} = 90^\circ \) (gt)

Do đó, \(\Delta ABM = \Delta DBM\) (ch – cgv)

b) Do \(\Delta ABM = \Delta DBM\) (cmt) nên \(AM = MD\) (hai cạnh tương ứng)

Xét \(\Delta AMN\) và \(\Delta DMC\), ta có:

\(\widehat {MAN} = \widehat {MDC} = 90^\circ \) (gt)

\(AM = MD\) (cmt)

\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)

Suy ra \(\Delta AMN = \Delta DMC\) (cgv – gn)

Do đó, \(MN = MC\) (hai cạnh tương ứng)

Suy ra \(\Delta MNC\) cân tại \(M.\)

c) Do \(\Delta MNC\) cân tại \(M\) và \(I\) là trung điểm của \(NC\) nên \(MI\) cũng là đường cao của \(\Delta MNC\).

Suy ra \(MI \bot NC\).

Xét \(\Delta AMN\) và \(\Delta DMC,\) có:

\(\widehat {AMN} = \widehat {DMC}\) (đối đỉnh)

\(AM = MD\) (cmt)

\(MN = MC\) (cmt)

Suy ra \(\Delta AMN = \Delta DMC\) (c.g.c)

Do đó, \(AN = DC\) (hai cạnh tương ứng)

Ta có: \(AB + AN = BN;{\rm{ }}BD + DC = BC\).

Mà \(AN = DC,AB = BD\). Suy ra \(BN = BC\).

Do đó, \(\Delta BNC\) cân tại \(B\).

Suy ra \(BI \bot NC\) tại \(I\).

Mà \(MI \bot NC\) tại \(I\).

Do đó, \(B,M,I\) thẳng hàng.

Hướng dẫn giải

Tổng số bông hoa trong hộp kín là \(10 + 20 + n = n + 30\) (bông)

Xác suất để lấy được một bông hoa hồng xanh là \(\frac{n}{{n + 30}}\).

Mà xác suất để lấy được một bông hoa hồng xanh là \(\frac{4}{{10}}\).

Do đó, ta có: \(\frac{n}{{n + 30}} = \frac{4}{{10}}\) hay \(10n = 4n + 120\), do đó \(6n = 120\) nên \(n = 20\).

Vậy trong hộp có 20 bông hoa hồng xanh.