(2,5 điểm) Danh sách tham dự kì thi “Hùng biện Tiếng anh” của lớp 7A có 10 bạn được xếp theo thứ tự từ 1 đến 10. Bạn Hùng đứng vị trí thứ 8 trong danh sách đó. Cô giáo chọn ngẫu nhiên một bạn làm đội trưởng.
a) Có bao nhiêu kết quả có thể xảy ra?
b) Cho biến cố “Cô giáo chọn được bạn có số thứ tự không lớn hơn số thứ tự của Hùng”. Nêu các kết quả thuận lợi của biến cố đó.
c) Tính xác suất của biến cố “Cô giáo chọn được bạn có số thứ tự lớn hơn Hùng”.
d) Bạn Hùng có bao nhiêu phần trăm được làm đội trưởng?
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 2 Toán 7 Cánh diều (Tự luận) có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Do danh sách dự thi “Hùng biện Tiếng anh” của lớp 7A có \(10\) bạn học sinh nên có \(10\) kết quả có thể xảy ra.
b) Các kết quả thuận lợi của biến cố “Cô giáo chọn được bạn có số thứ tự không lớn hơn số thứ tự của Hùng” là:
các bạn được đánh số \(\left\{ {1;2;3;4;5;6;7;8} \right\}\). Do đó, có 8 kết quả thuận lợi.
c) Các kết quả thuận lợi của biến cố “Cô giáo chọn được bạn có số thứ tự lớn hơn Hùng” là: \(\left\{ {9;10} \right\}\).
Do đó, xác suất của biến cố trên là: \(\frac{2}{{10}} = \frac{1}{5}\).
d) Xác suất để chọn được bạn Hùng làm đội trưởng là: \(\frac{1}{{10}} = 10\% \).
Do đó, có \(10\% \) để bạn Hùng được làm đội trưởng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
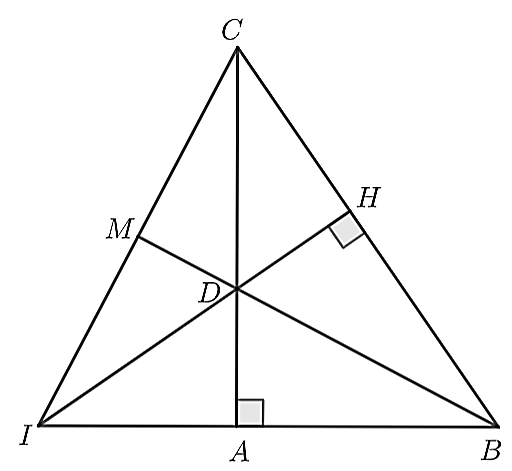
a) Xét
\(\Delta ABD\) và \(\Delta HBD\), có:
\(\widehat {ABD} = \widehat {DBH}\) (\(BD\) là phân giác của \(\widehat B\))
\(BD\) chung (gt)
\(\widehat {DAB} = \widehat {DHB} = 90^\circ \) (gt)
Suy ra \(\Delta ABD = \Delta HBD\) (ch – gn)
Do đó, \(AB = BH\) (hai cạnh tương ứng).
Suy ra \(\Delta ABH\) cân tại \(B\) có \(BD\) là tia phân giác \(\widehat B\).
Suy ra \(BD\) cũng là đường trung trực của \(AH\). Do đó, \(BD \bot AH.\)
b) Do \(\Delta ABD = \Delta HBD\) (cmt) nên \[DA = DH\] (hai cạnh tương ứng)
Xét tam giác \[DAH\] vuông tại \[H\] nên có \[DA\] là cạnh huyền.
Do đó, \[DA > DH\].
Từ đó, suy ra \(DC > AD.\)
c) Chứng minh được \(\Delta ADI = \Delta HDC\) (cgv – gn)
Suy ra \(IA = CH\) (hai cạnh tương ứng)
Mà có \(AB = BH\), suy ra \(AB + AI = BH + HC\) hay \(BI = BC\).
Xét \(\Delta BIM\) và \(\Delta BCM\), có:
\(MI = MC\) (gt)
\(BM\) chung (gt)
\(BI = BC\) (cmt)
Suy ra \(\Delta BIM = \Delta BCM\) (c.c.c)
Do đó, \(\widehat {IBM} = \widehat {CBM}\) (hai góc tương ứng)
Suy ra \(BM\) là phân giác của \(\widehat {ABC}\).
Mà \(BD\) cũng là phân giác của \(\widehat {ABC}\).
Suy ra \(B,D,M\) thẳng hàng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Theo đề, gọi xác suất của biến cố “Lan lấy được quả bóng màu xanh” là \(n\).
Vì biến cố “Lan lấy được quả bóng màu đỏ”, “Lan lấy được quả bóng màu xanh” và “Lan lấy được quả bóng màu vàng” là ba biến cố đồng khả năng.
Do đó, xác suất của ba biến cố này bằng nhau và bằng \(n\).
Từ đó, ta có: \(n + n + n = 1\) hay \(3n = 1\), suy ra \(n = \frac{1}{3}\).
Gọi số quả bóng của màu xanh là \(x,\) ta có: \(\frac{x}{{60}} = \frac{1}{3}\) hay \(x = 20\).
Tương tự ta tính được số quả bóng đỏ và vàng cũng bằng \(20\).
Do đó, số quả bóng màu xanh, đỏ và vàng đều bằng \(20\) quả.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập