2.1. Giáo viên tổng phụ trách khối 9 đã thống kê được số học sinh tham gia và đạt kết quả trong các cuộc thi thể thao và thu được kết quả như sau:

Bộ môn	Cầu lông	Bóng rổ	Chạy bền	Nhảy xa	Bóng chuyền
Nam đạt giải	5	3	4	6	7
Nữ đạt giải	4	5	2	3	4
Nam tham gia	12	8	10	9	11
Nữ tham gia	9	10	7	8	6

Hãy sử dụng dữ liệu trên để trả lời các câu hỏi sau:

     a) Có bao nhiêu học sinh nam tham gia các cuộc thi? Bao nhiêu học sinh nữ tham gia các cuộc thi?

     b) Chọn ngẫu nhiên một học sinh nam tham gia thi, tính xác suất để học sinh đó đạt giải ở bộ môn chạy bền.

     c) Chọn ngẫu nhiên một học sinh tham gia thi, tính xác suất học sinh đó đạt giải ở bộ môn cầu lông.

     2.2. Tại kì rút thăm trúng thưởng của một cửa hàng, khách hàng phải rút thăm và lập được số có hai chữ số lớn hơn 90 để trúng thưởng. Người ta làm một chiếc lọ đựng 9 lá thăm cùng kích thước, vật liệu, có ghi các số từ 1 đến 9. Đầu tiên, khách hàng rút ngẫu nhiên 1 lá thăm, ghi số ở lá thăm rút được vào hàng đơn vị của số cần tìm, rồi trả lại lá thăm vào lọ. Tiếp tục rút ngẫu nhiên 1 lá thăm rồi ghi số ở lá thăm rút được vào hàng chục của số cần tìm.

     a) Tìm số phần tử của không gian mẫu.

     b) Tính xác suất của biến cố “Khách hàng lập được số nguyên tố nhỏ hơn 20”

     a)

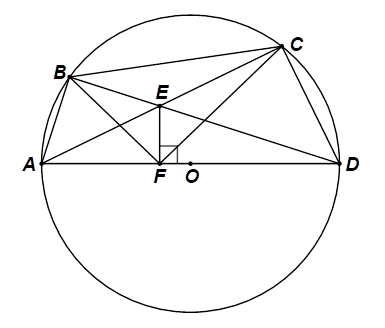
Vì điểm \(B\) nằm trên đường tròn đường kính \(AD\) nên \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Do \(\Delta ABE\) vuông tại \(B\) nên đường tròn ngoại tiếp tam giác có tâm là trung điểm \(AE\) hay đường tròn ngoại tiếp tam giác \(ABE\) có đường kính \(AE\).

Tương tự, \(EF \bot AD\) nên \(\Delta AEF\) vuông tại \(F,\) có đường tròn ngoại tiếp tam giác là đường tròn đường kính \(AE.\)

Do đó, các điểm \(A,\,\,B,\,\,E,\,\,F\) đều nằm trên đường tròn đường kính \(AE.\)

Vậy tứ giác \(ABEF\) nội tiếp đường tròn đường kính \(AE.\)

       b) Tứ giác \(ABEF\) nội tiếp nên \(\widehat {BAE} = \widehat {BFE}\) (hai góc nội tiếp cùng chắn cung \(BE).\) (1)

Chứng minh tương tự câu a) ta có tứ giác \(CDFE\) nội tiếp đường tròn đường kính \(DE.\)

Suy ra \(\widehat {EFC} = \widehat {EDC}\) (hai góc nội tiếp cùng chắn cung \(EC).\) (2)

Lại có tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(\widehat {BAC} = \widehat {BDC}\) (hai góc nội tiếp cùng chắn cung \(BC)\) hay \(\widehat {BAE} = \widehat {EDC}.\) (3)

Từ (1), (2), (3) suy ra \(\widehat {BFE} = \widehat {EFC}\) hay \(FE\) là tia phân giác của \(\widehat {BFC}.\)

Chứng minh tương tự như trên, ta có \(BD\) là tia phân giác của \(\widehat {CBF}.\)

Xét \(\Delta BCF\) có \(BD,\,\,FE\) là hai đường phân giác của tam giác cắt nhau tại \(E\) nên \(E\) là giao điểm ba đường phân giác của tam giác này.

Do đó \(E\) là tâm đường tròn nội tiếp tam giác \(BCF.\)

     a) Đối tượng thống kê là số học sinh lớp 9B trong học kì I và II.

    Tiêu chí thống kê là học lực của các bạn học sinh lớp 9B gồm: Tốt, Khá và Đạt.

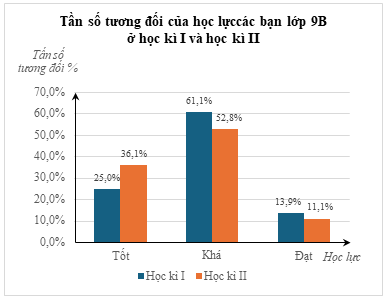
     b) Số học sinh của lớp 9B là: \[9 + 22 + 5 = 36\] (học sinh)

    So với kì I, học lực Tốt của lớp 9B tăng, học lực Khá và Đạt của lớp 9B giảm.

     c) Từ bảng thống kê trên ta tính được tần số tương đối của hai đối tượng khác nhau nên dùng biểu đồ tần số tương đối ở dạng cột kép để biểu diễn dữ liệu.

Ta lập bảng tần số tương đối như sau:

     d) Biểu đồ tần số tương đối dạng cột kép: