3.1. Người ta muốn dựng khung cổng hình chữ nhật rộng \(4{\rm{\;m}}\) và cao \(3{\rm{\;m}}{\rm{,}}\) bên ngoài được bao bởi một khung thép dạng nửa đường tròn. Tính chiều dài (đơn vị mét) của đoạn thép làm khung nửa đường tròn đó.

3.2. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {2;\,\,3} \right).\) Thực hiện phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ. Xác tọa độ của điểm \(A\) sau khi quay.
3.1. Người ta muốn dựng khung cổng hình chữ nhật rộng \(4{\rm{\;m}}\) và cao \(3{\rm{\;m}}{\rm{,}}\) bên ngoài được bao bởi một khung thép dạng nửa đường tròn. Tính chiều dài (đơn vị mét) của đoạn thép làm khung nửa đường tròn đó.

3.2. Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(A\left( {2;\,\,3} \right).\) Thực hiện phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ. Xác tọa độ của điểm \(A\) sau khi quay.
Quảng cáo
Trả lời:
3.1. Giả sử \[ABCD\] là khung cổng hình chữ nhật \[(AB = CD = 3{\rm{\;m}}\] và \[AD = BC = 4{\rm{\;m}})\] nội tiếp nửa đường tròn \[\left( O \right)\] (hình vẽ).
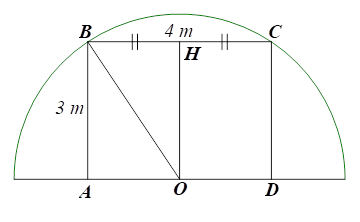
Gọi \[H\] là trung điểm của \[CD.\]
Khi đó \(HB = HC = \frac{1}{2}BC = \frac{1}{2} \cdot 4 = 2{\rm{\;(m)}}\) và \[H\] nằm trên đường trung trực của \[BC.\]
Vì \[B,{\rm{ }}C\] cùng nằm trên nửa đường tròn \[\left( O \right)\] nên \[OB = OC,\] suy ra \[O\] nằm trên đường trung trực của \[BC.\]
Do đó \[OH\] là đường trung trực của đoạn thẳng \[BC,\] nên \[OH \bot BC.\]
Mà \[BC\,{\rm{//}}\,AD\] (do \[ABCD\] là hình chữ nhật) nên \[OH \bot AD.\]
Xét tứ giác \[ABHO\] có \(\widehat {OAB} = \widehat {AOH} = \widehat {OHB} = 90^\circ \) nên \[ABHO\] là hình chữ nhật.
Do đó \[OH = AB = 3{\rm{\;(m)}}{\rm{.}}\]
Xét \(\Delta OBH\) vuông tại \[H,\] theo định lí Pythagore, ta có: \(O{B^2} = O{H^2} + H{B^2} = {3^2} + {2^2} = 13.\)
Do đó \(OB = \sqrt {13} {\rm{\;m}}.\)
Nửa chu vi đường tròn \[\left( O \right)\] là: \[\pi \sqrt {13} {\rm{\;\;(m)}}{\rm{.}}\]
3.2. Ta có hình vẽ sau:
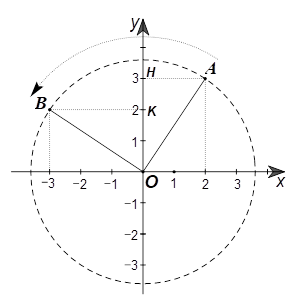
Gọi \[H\] là hình chiếu của \[A\] trên \[Oy.\] Ta có \(A\left( {2;\,\,3} \right)\) nên \(AH = \left| 2 \right| = 2\) và \[OH = \left| 3 \right| = 3.\]
Xét \[\Delta AOH\] vuông tại \[H,\] theo định lí Pythagore ta có: \[O{A^2} = O{H^2} + A{H^2}\]
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} .\)
Ta cũng có \(\sin \widehat {AOH} = \frac{{AH}}{{OA}} = \frac{2}{{\sqrt {13} }}.\)
Giả sử phép quay \(90^\circ \) ngược chiều kim đồng hồ quanh gốc tọa độ biến điểm \(A\) (ở góc phần tư thứ I) thành điểm \(B\). Khi đó, điểm \(B\) nằm ở góc phần tư thứ II và \(OB = OA = \sqrt {13} ,\,\,\widehat {AOB} = 90^\circ .\)
Ta có \(\widehat {AOB} = \widehat {AOH} + \widehat {BOH} = 90^\circ \) nên \(\cos \widehat {BOH} = \sin \widehat {AOH} = \frac{2}{{\sqrt {13} }}.\)
Xét \(\Delta OBK\) vuông tại \(K\) (gọi \(K\) là hình chiếu của điểm \(B\) trên \(Oy)\) ta có:
\(OK = OB \cdot \cos \widehat {BOH} = \sqrt {13} \cdot \frac{2}{{\sqrt {13} }} = 2.\)
Từ đó, ta có tung độ của điểm \(B\) là \(2\) (do \(B\) nằm ở góc phần tư thứ II).
Tương tự, ta tìm được hoành độ của điểm \(B\) là \( - 3.\)\(\)
Như vậy, phép quay ngược chiều \[90^\circ \] tâm \[O\] biến điểm \(A\left( {2;\,\,3} \right)\) thành điểm \[B\left( {--3;{\rm{ }}2} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
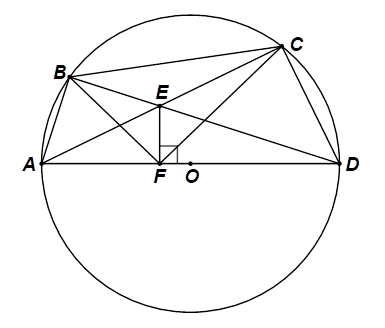
Vì điểm \(B\) nằm trên đường tròn đường kính \(AD\) nên \(\widehat {ABD} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Do \(\Delta ABE\) vuông tại \(B\) nên đường tròn ngoại tiếp tam giác có tâm là trung điểm \(AE\) hay đường tròn ngoại tiếp tam giác \(ABE\) có đường kính \(AE\).
Tương tự, \(EF \bot AD\) nên \(\Delta AEF\) vuông tại \(F,\) có đường tròn ngoại tiếp tam giác là đường tròn đường kính \(AE.\)
Do đó, các điểm \(A,\,\,B,\,\,E,\,\,F\) đều nằm trên đường tròn đường kính \(AE.\)
Vậy tứ giác \(ABEF\) nội tiếp đường tròn đường kính \(AE.\)
b) Tứ giác \(ABEF\) nội tiếp nên \(\widehat {BAE} = \widehat {BFE}\) (hai góc nội tiếp cùng chắn cung \(BE).\) (1)
Chứng minh tương tự câu a) ta có tứ giác \(CDFE\) nội tiếp đường tròn đường kính \(DE.\)
Suy ra \(\widehat {EFC} = \widehat {EDC}\) (hai góc nội tiếp cùng chắn cung \(EC).\) (2)
Lại có tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) nên \(\widehat {BAC} = \widehat {BDC}\) (hai góc nội tiếp cùng chắn cung \(BC)\) hay \(\widehat {BAE} = \widehat {EDC}.\) (3)
Từ (1), (2), (3) suy ra \(\widehat {BFE} = \widehat {EFC}\) hay \(FE\) là tia phân giác của \(\widehat {BFC}.\)
Chứng minh tương tự như trên, ta có \(BD\) là tia phân giác của \(\widehat {CBF}.\)
Xét \(\Delta BCF\) có \(BD,\,\,FE\) là hai đường phân giác của tam giác cắt nhau tại \(E\) nên \(E\) là giao điểm ba đường phân giác của tam giác này.
Do đó \(E\) là tâm đường tròn nội tiếp tam giác \(BCF.\)
Lời giải
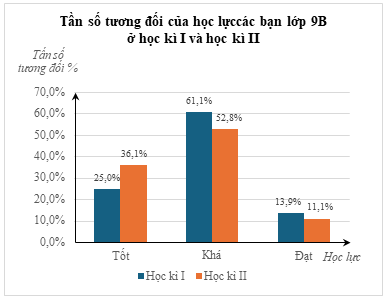
a) Đối tượng thống kê là số học sinh lớp 9B trong học kì I và II.
Tiêu chí thống kê là học lực của các bạn học sinh lớp 9B gồm: Tốt, Khá và Đạt.
b) Số học sinh của lớp 9B là: \[9 + 22 + 5 = 36\] (học sinh)
So với kì I, học lực Tốt của lớp 9B tăng, học lực Khá và Đạt của lớp 9B giảm.
c) Từ bảng thống kê trên ta tính được tần số tương đối của hai đối tượng khác nhau nên dùng biểu đồ tần số tương đối ở dạng cột kép để biểu diễn dữ liệu.
Ta lập bảng tần số tương đối như sau:
|
Học lực |
Tốt |
Khá |
Đạt |
|
Học kì I |
\[25\% \] |
\(61,1\% \) |
\(13,9\% \) |
|
Học kì II |
\(36,1\% \) |
\(52,8\% \) |
\(11,1\% \) |
d) Biểu đồ tần số tương đối dạng cột kép:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.