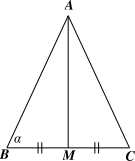
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = 2a\) và \(\widehat {B\,} = \alpha \). Tính diện tích tam giác \(ABC\).

Hướng dẫn giải

Gọi \(x{\rm{\;(kg)}}\) là khối lượng axit \(X\) có trong dung dịch \(A\) và \(y{\rm{\;(kg)}}\) là khối lượng dung dịch chất \(A\) \(\left( {y > x > 0} \right)\).

Khi thêm \[1\] kg nước vào dung dịch \[A\] thì được dung dịch \[B\] có khối lượng là: \(y + 1{\rm{\;(kg)}}\).

Theo bài, nồng độ của dung dịch \(B\) là \[20\% \] nên ta có phương trình:

\(\frac{x}{{y + 1}} \cdot 100\% = 20\% \) hay \(5x = y + 1\) suy ra \(5x - y = 1\) (1)

Khi thêm \[1\] kg axit vào dung dịch \[B\] thì được dung dịch \[C\] có khối lượng là: \(y + 1 + 1 = y + 2{\rm{\;(kg)}}\) và khối lượng axit \(X\) có trong dung dịch lúc này là \(x + 1{\rm{\;(kg)}}\)

Theo bài, nồng độ của dung dịch \(C\) là \[33\frac{1}{3}\% \] nên ta có phương trình:

\(\frac{{x + 1}}{{y + 2}} \cdot 100\% = 33\frac{1}{3}\% \) hay \(3\left( {x + 1} \right) = y + 2\) suy ra \(3x - y = - 1\). (2)

Từ phương trình (1) và phương trình (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}5x - y = 1\\3x - y = - 1\end{array} \right.\)

Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:

\(2x = 2,\) suy ra \(x = 1\) (thỏa mãn).

Thay \(x = 1\) vào phương trình \(5x = y + 1\) ta được:

\(5 \cdot 1 = y + 1\), suy ra \(y = 4\) (thỏa mãn).

Vậy nồng độ axit của dung dịch \(A\) là: \(\frac{x}{y} \cdot 100\% = \frac{1}{4} \cdot 100\% = 25\% .\)

Đáp án đúng là: D

Ta viết phương trình \(2x - y = 1\) về dạng \(y = 2x - 1\).

⦁ Xét cặp số \(\left( {1;\,\,0} \right),\) thay \(x = 1\) vào phương trình \(y = 2x - 1\), ta được: \(y = 2 \cdot 1 - 1 = 1 \ne 0.\)

Do đó, cặp số \(\left( {1;\,\,0} \right)\) không phải là nghiệm của phương trình \(2x - y = 1\), hay đường thẳng \(y = 2x - 1\) không đi qua điểm \(\left( {1;\,\,0} \right)\). Do đó đường thẳng \({d_1},\,\,{d_3}\) không thỏa mãn.

⦁ Xét cặp số \(\left( {0;\,\, - 1} \right),\) thay \(x = 0\) và \(y = - 1\) vào phương trình \(y = 2x - 1\), ta được:

\(y = 2x - 1 = 2 \cdot 0 - 1 = - 1\).

Do đó, cặp số \(\left( {0;\,\, - 1} \right)\) là nghiệm của phương trình \(2x - y = 1\), hay đường thẳng \(y = 2x - 1\) đi qua điểm \(\left( {0;\,\, - 1} \right)\).

Quan sát hình b) và hình d) ta thấy chỉ có đường thẳng \({d_4}\) thỏa mãn.

Vậy ta chọn phương án D.