(1,5 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Người ta cho thêm \[1\] kg nước vào dung dịch \[A\] (của axit \(X)\) thì được dung dịch \[B\] có nồng độ axit là \[20\% \]. Sau đó lại cho thêm \[1\] kg axit \(X\) vào dung dịch \[B\] thì được dung dịch \[C\] có nồng độ axit là \[33\frac{1}{3}\% \]. Tính nồng độ axit của dung dịch \[A\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi \(x{\rm{\;(kg)}}\) là khối lượng axit \(X\) có trong dung dịch \(A\) và \(y{\rm{\;(kg)}}\) là khối lượng dung dịch chất \(A\) \(\left( {y > x > 0} \right)\).
Khi thêm \[1\] kg nước vào dung dịch \[A\] thì được dung dịch \[B\] có khối lượng là: \(y + 1{\rm{\;(kg)}}\).
Theo bài, nồng độ của dung dịch \(B\) là \[20\% \] nên ta có phương trình:
\(\frac{x}{{y + 1}} \cdot 100\% = 20\% \) hay \(5x = y + 1\) suy ra \(5x - y = 1\) (1)
Khi thêm \[1\] kg axit vào dung dịch \[B\] thì được dung dịch \[C\] có khối lượng là: \(y + 1 + 1 = y + 2{\rm{\;(kg)}}\) và khối lượng axit \(X\) có trong dung dịch lúc này là \(x + 1{\rm{\;(kg)}}\)
Theo bài, nồng độ của dung dịch \(C\) là \[33\frac{1}{3}\% \] nên ta có phương trình:
\(\frac{{x + 1}}{{y + 2}} \cdot 100\% = 33\frac{1}{3}\% \) hay \(3\left( {x + 1} \right) = y + 2\) suy ra \(3x - y = - 1\). (2)
Từ phương trình (1) và phương trình (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}5x - y = 1\\3x - y = - 1\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\(2x = 2,\) suy ra \(x = 1\) (thỏa mãn).
Thay \(x = 1\) vào phương trình \(5x = y + 1\) ta được:
\(5 \cdot 1 = y + 1\), suy ra \(y = 4\) (thỏa mãn).
Vậy nồng độ axit của dung dịch \(A\) là: \(\frac{x}{y} \cdot 100\% = \frac{1}{4} \cdot 100\% = 25\% .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \({d_1}\).
B. \({d_2}\).
C. \({d_3}\).
D. \({d_4}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Ta viết phương trình \(2x - y = 1\) về dạng \(y = 2x - 1\).
⦁ Xét cặp số \(\left( {1;\,\,0} \right),\) thay \(x = 1\) vào phương trình \(y = 2x - 1\), ta được: \(y = 2 \cdot 1 - 1 = 1 \ne 0.\)
Do đó, cặp số \(\left( {1;\,\,0} \right)\) không phải là nghiệm của phương trình \(2x - y = 1\), hay đường thẳng \(y = 2x - 1\) không đi qua điểm \(\left( {1;\,\,0} \right)\). Do đó đường thẳng \({d_1},\,\,{d_3}\) không thỏa mãn.
⦁ Xét cặp số \(\left( {0;\,\, - 1} \right),\) thay \(x = 0\) và \(y = - 1\) vào phương trình \(y = 2x - 1\), ta được:
\(y = 2x - 1 = 2 \cdot 0 - 1 = - 1\).
Do đó, cặp số \(\left( {0;\,\, - 1} \right)\) là nghiệm của phương trình \(2x - y = 1\), hay đường thẳng \(y = 2x - 1\) đi qua điểm \(\left( {0;\,\, - 1} \right)\).
Quan sát hình b) và hình d) ta thấy chỉ có đường thẳng \({d_4}\) thỏa mãn.
Vậy ta chọn phương án D.
Câu 2
A. \(\frac{1}{3}\).
B. \(\frac{{2\sqrt 2 }}{3}\).
C. \(2\sqrt 2 \).
D. \(\frac{{\sqrt 2 }}{4}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
Xét \(\Delta ABC\) vuông tại \(A\), theo định lí Pythagore, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
Suy ra \(A{C^2} = B{C^2} - A{B^2} = {15^2} - {5^2} = 200\)
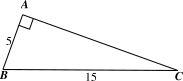
Do đó \(AC = \sqrt {200} = \sqrt {100 \cdot 2} = \sqrt {{{10}^2} \cdot {{\left( {\sqrt 2 } \right)}^2}} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2}} = 10\sqrt 2 \).
Khi đó \(\tan B = \frac{{AC}}{{AB}} = \frac{{10\sqrt 2 }}{5} = 2\sqrt 2 .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập