Cho các nội dung sau:
(1) Tìm điều kiện xác định của phương trình.
(2) Xét mỗi giá trị tìm được của ẩn, giá trị nào thỏa mãn điều kiện xác định thì đó là nghiệm của phương trình đã cho.
(3) Giải phương trình vừa nhận được.
(4) Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu.
Sắp xếp các nội dung trên theo thứ tự các bước để giải phương trình chứa ẩn ở mẫu là
A. (1), (2), (3), (4).
B. (1), (3), (2), (4).
C. (1), (4), (2), (3).
D. (1), (4), (3), (2).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 9 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Các bước để giải phương trình chứa ẩn ở mẫu là
(1) Tìm điều kiện xác định của phương trình.
(4) Quy đồng mẫu thức hai vế của phương trình rồi khử mẫu.
(3) Giải phương trình vừa nhận được.
(2) Xét mỗi giá trị tìm được của ẩn, giá trị nào thỏa mãn điều kiện xác định thì đó là nghiệm của phương trình đã cho.
Vậy ta chọn phương án D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải

Xét \(\Delta ABC\) vuông tại \(A\) có \(\widehat {B\,} = \alpha \).
Do \(\widehat {B\,}\) là góc nhọn nên \(0^\circ < \widehat {B\,} < 90^\circ \) hay \[0^\circ < \alpha < 90^\circ .\]
Ta có: \(\sin \alpha = \frac{{AC}}{{BC}}\) và \(\cos \alpha = \frac{{AB}}{{BC}}.\)
\(B{C^2} = A{B^2} + A{C^2}\) (định lí Pythagore).
Khi đó: \[{\sin ^2}\alpha + {\cos ^2}\alpha = {\left( {\frac{{AC}}{{BC}}} \right)^2} + {\left( {\frac{{AB}}{{BC}}} \right)^2} = \frac{{A{C^2}}}{{B{C^2}}} + \frac{{A{B^2}}}{{B{C^2}}} = \frac{{A{C^2} + A{B^2}}}{{B{C^2}}} = \frac{{B{C^2}}}{{B{C^2}}} = 1.\]
Với \[0^\circ < \alpha < 90^\circ \] thì \[1 - \cos \alpha \ne 0\] và \[\sin \alpha - \cos \alpha + 1 \ne 0\].
Ta có: \[\frac{{\sin \alpha + \cos \alpha - 1}}{{1 - \cos \alpha }} - \frac{{2\cos \alpha }}{{\sin \alpha - \cos \alpha + 1}}\]
\[ = \frac{{\left( {\sin \alpha + \cos \alpha - 1} \right)\left( {\sin \alpha - \cos \alpha + 1} \right) - 2\cos \alpha \left( {1 - \cos \alpha } \right)}}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{\left[ {\sin \alpha + \left( {\cos \alpha - 1} \right)} \right]\left[ {\sin \alpha - \left( {\cos \alpha - 1} \right)} \right] - 2\cos \alpha \left( {1 - \cos \alpha } \right)}}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - {{\left( {\cos \alpha - 1} \right)}^2} - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - \left( {{{\cos }^2}\alpha - 2\cos \alpha + 1} \right) - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}\alpha - {{\cos }^2}\alpha + 2\cos \alpha - 1 - 2\cos \alpha + 2{{\cos }^2}\alpha }}{{\left( {1 - \cos \alpha } \right)\left( {\sin \alpha - \cos \alpha + 1} \right)}}\]
\[ = \frac{{{{\sin }^2}x + {{\cos }^2}x - 1}}{{\left( {1 - \cos x} \right)\left( {\sin x - \cos x + 1} \right)}}.\]
\[ = \frac{{1 - 1}}{{\left( {1 - \cos x} \right)\left( {\sin x - \cos x + 1} \right)}} = 0\] (vì \[1 - \cos x \ne 0\] và \[\sin x - \cos x + 1 \ne 0)\]
Vậy \[\frac{{\sin x + \cos x - 1}}{{1 - \cos x}} = \frac{{2\cos x}}{{\sin x - \cos x + 1}}.\]
Lời giải
1. Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
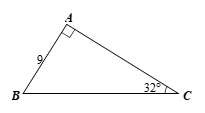
⦁ \(\sin C = \frac{{AB}}{{BC}},\) suy ra \(BC = \frac{{AB}}{{\sin C}} = \frac{9}{{\sin 32^\circ }} \approx 16,98.\)
⦁ \(AC = AB \cdot \cot C = 9 \cdot \cot 32^\circ \approx 14,40.\)
Vậy \[AC \approx 14,40\] và \[BC \approx 16,98.\]
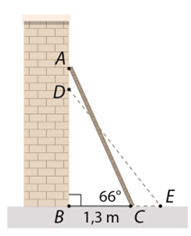
2. Xét \(\Delta ABC\) vuông tại \(A,\) ta có:
\(BC = AC \cdot \cos C\), suy ra \(AC = \frac{{BC}}{{\cos C}} = \frac{{1,3}}{{\cos 66^\circ }} \approx 3,20\) (m).
Xét \(\Delta ABC\) vuông tại \(A,\) ta có: \(AB = BC \cdot \tan C = 1,3 \cdot \tan 66^\circ \approx 2,92\) (m).
Khi đầu \(A\) của thang bị trượt xuống \(40{\rm{\;cm}} = 0,4{\rm{\;m}}\) đến vị trí \(D\) thì \(DB = AB - AD \approx 2,92 - 0,4 = 2,52\) (m) và chiều dài thang là \(DE = AC \approx 3,20\) (m).
Xét \(\Delta BDE\) vuông tại \(B,\) ta có:
\(\sin \widehat {DEB} = \frac{{BD}}{{DE}} \approx \frac{{2,52}}{{3,2}} = 0,7875\), suy ra \(\widehat {DEB} \approx 51^\circ 57'.\)
Câu 3
A. \(\frac{{\sqrt 3 }}{2}.\)
B. \(\frac{1}{2}\).
C. \(\frac{{\sqrt 2 }}{2}.\)
D. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\tan \alpha = \cot \beta .\)
B. \(\tan \alpha = \sin \beta .\)
C. \(\tan \alpha = \cos \beta .\)
D. \(\tan \alpha = \tan \beta .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.