Tìm 𝛼, 𝛽 để hàm số \[h\left( x \right) = \sqrt {1 - 2x} - 1 - \ln \left( {1 - x} \right) \sim \alpha {x^\beta }\] khi 𝑥 → 0.

A. I = 0

B. I = 1

D. \[I = \sqrt e \]

A. Hàm số không có cực trị.

B. Hàm số đạt cực trị tại 𝑥 = 1; và cực tiểu tại 𝑥 = 3.

C. Hàm số đạt cực trị tại 𝑥 = 3; và cực tiểu tại 𝑥 = 1.

D. Hàm số đạt cực trị tại 𝑥 = −1; và cực tiểu tại 𝑥 = 1.

A. α = e^-2

A. \[{y_{\max }} = 16,{y_{\min }} = 0\]

B. \[{y_{\max }} = 0,{y_{\min }} = 16\]

C. \[{y_{\max }} = 2,{y_{\min }} = - 2\sqrt 2 \]

D. Các câu khác sai

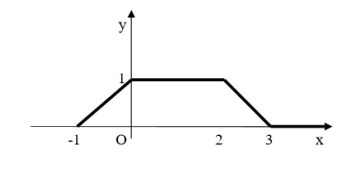
A.\[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 < x < 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,0 \le x \le 2}\\{ - x + 3,2 < x \le 3}\\{0,\,\,\,\,\,\,3 \ge x}\end{array}} \right.\]</>

B. \[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 \le x \le 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2}\\{ - x + 3,2 < x \le 3}\\{0,\,\,\,\,3 \le x}\end{array}} \right.\]

</>

C. \[f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x + 1, - 1 < x \le 0}\\{1,\,\,\,\,\,\,\,\,\,\,\,\,\,0 < x \le 2}\\{ - x - 3,2 < x \le 3}\\{0,\,\,\,\,3 \le x}\end{array}} \right.\]

D. Không có câu nào có đáp án đúng.

A. Đáp án khác.

B. 0,0232.

C. 0,0757.

D. 0,0428.

A. \[\left[ {0;\frac{{\sqrt \pi }}{2}} \right)\]

B. \[\left[ {0;\frac{{\sqrt \pi }}{2}} \right]\]

C. \[\left( {0;\frac{{\sqrt \pi }}{2}} \right)\]

D. \[\left( {0;\frac{\pi }{2}} \right)\]