(0,5 điểm) Cho \(C = \frac{3}{{{1^2}{{.2}^2}}} + \frac{5}{{{2^2}{{.3}^2}}} + \frac{7}{{{3^2}{{.4}^2}}} + .... + \frac{{4047}}{{{{2023}^2}{{.2024}^2}}}\). Chứng minh \(C < 1.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Ta có: \(C = \frac{3}{{{1^2}{{.2}^2}}} + \frac{5}{{{2^2}{{.3}^2}}} + \frac{7}{{{3^2}{{.4}^2}}} + .... + \frac{{4047}}{{{{2023}^2}{{.2024}^2}}}\)
\(C = \frac{{{2^2} - {1^2}}}{{{1^2}{{.2}^2}}} + \frac{{{3^2} - {2^2}}}{{{2^2}{{.3}^2}}} + \frac{{{4^2} - {3^2}}}{{{3^2}{{.4}^2}}} + .... + \frac{{{{2024}^2} - {{2023}^2}}}{{{{2023}^2}{{.2024}^2}}}\)
\(C = \frac{1}{{{1^2}}} - \frac{1}{{{2^2}}} + \frac{1}{{{2^2}}} - \frac{1}{{{3^2}}} + \frac{1}{{{3^2}}} - \frac{1}{{{4^2}}} + .... + \frac{1}{{{{2023}^2}}} - \frac{1}{{{{2024}^2}}}\)
\(C = \frac{1}{{{1^2}}} - \frac{1}{{{{2024}^2}}}\)
\(C = 1 - \frac{1}{{{{2024}^2}}}\)
Nhận thấy \(\frac{1}{{{1^2}}} - \frac{1}{{{{2024}^2}}} < 1\) nên \(C < 1\) (đpcm).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đ b) Đ c) S d) Đ
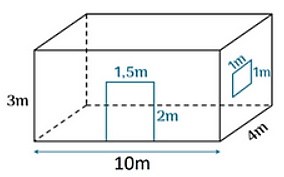
• Tổng diện tích các cửa của căn phòng này là: \(1,5.2 + 1.1 = 4\) (m2).
Do đó, ý a) là đúng.
• Diện tích xung quanh của căn phòng là: \(2.\left( {10 + 4} \right).3 = 84\) (m2).
Do đó, ý b) là đúng.
• Diện tích của trần nhà là: \(4.10 = 40\) (m2)
Tổng diện tích cần sơn của căn phòng là: \(40 + 84 - 4 = 120\) (m2).
Do đó, ý c) là sai.
• Chi phí bác An cần để sơn căn phòng đó là: \(250{\rm{ }}000.120 = 30{\rm{ }}000{\rm{ }}000\) (đồng).
Vậy chi phí bác An cần để sơn căn phòng đó là 30 triệu đồng.
Do đó, ý d) là đúng.
Lời giải
Hướng dẫn giải
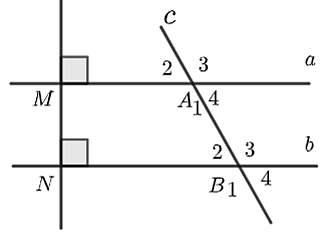
a) Nhận thấy \(\widehat M = \widehat N = 90^\circ \) (giả thiết).
Mà hai góc ở vị trí đồng vị nên \(a\parallel b\).
b) Vì \(a\parallel b\) nên \(\widehat {{A_2}} = \widehat {{B_2}} = 55^\circ \) (đồng vị).
Lại có \(\widehat {{B_2}}\) và \(\widehat {{B_3}}\) là hai góc kề bù.
Do đó, \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) nên \(\widehat {{B_3}} = 180^\circ - \widehat {{B_2}} = 180^\circ - 55^\circ = 125^\circ \).
c)
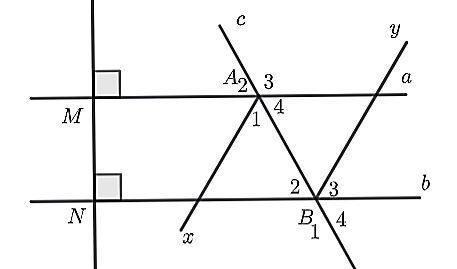
Ta có \(\widehat {{A_2}}\) và \(\widehat {{A_3}}\) kề bù nên \(\widehat {{A_3}} = 180^\circ - \widehat {{A_2}} = 180^\circ - 55^\circ = 125^\circ \).
Vì \(Ax\) là tia phân giác của \(\widehat {MAB}\) nên \(\widehat {MAx} = \widehat {xAB} = \frac{{\widehat {MAB}}}{2} = \frac{{125^\circ }}{2} = 62,5^\circ \).
Vì \(By\) là tia phân giác của \(\widehat {ABb}\) nên \(\widehat {ABy} = \widehat {yBb} = \frac{{\widehat {ABb}}}{2} = \frac{{125^\circ }}{2} = 62,5^\circ \).
Ta có \(\widehat {xAB} = \widehat {ABy} = 62,5^\circ \).
Mà hai góc ở vị trí so le trong nên \(Ax\parallel By.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập