Cho đa thức \(G = \left( {7{x^5}{y^4}{z^3} - 3{x^4}y{z^2} + 2{x^2}{y^2}z} \right):{x^2}yz\).
Đa thức \[A\] thỏa mãn \(A + 14{x^3}{y^3}{z^2} - 6{x^2}z = G\).
a) Bậc của đa thức \(G\) là 8.
b) Giá trị của biểu thức \(G\) tại \(x = 1\,;\,\,y = - 1\,;\,\,z = 1\) là 12.
c) Đa thức \[A\] có hạng tử tự do là 2.
d) Tổng của hai đa thức \[A\] và \(G\) là một đơn thức.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án:
a) Đúng.
b) Sai.
c) Sai.
d) Đúng.
⦁ Ta có \[G = \left( {7{x^5}{y^4}{z^3} - 3{x^4}y{z^2} + 2{x^2}{y^2}z} \right):{x^2}yz\]
\[ = 7{x^5}{y^4}{z^3}:{x^2}yz - 3{x^4}y{z^2}:{x^2}yz + 2{x^2}{y^2}z:{x^2}yz\]
\[ = 7{x^3}{y^3}{z^2} - 3{x^2}z + 2y\].
Đa thức \(G\) có bậc là 8. Do đó ý a) đúng.
⦁ Thay \(x = 1\,;\,\,y = - 1\,;\,\,z = 1\) vào biểu thức \(G\), ta có:
\(G = 7 \cdot {1^3} \cdot {\left( { - 1} \right)^3} \cdot {1^2} - 3 \cdot {1^2} \cdot 1 + 2 \cdot \left( { - 1} \right) = - 7 - 3 - 2 = - 12.\)
Vậy với \(x = 1\,;\,\,y = - 1\,;\,\,z = 1\) thì \(G = - 12\). Do đó ý b) sai.
⦁ Ta có \(A + 14{x^3}{y^3}{z^2} - 6{x^2}z = G\) hay \(A + 14{x^3}{y^3}{z^2} - 6{x^2}z = 7{x^3}{y^3}{z^2} - 3{x^2}z + 2y\)
Suy ra \(A = \left( {7{x^3}{y^3}{z^2} - 3{x^2}z + 2y} \right) - 2y\)
\( = 7{x^3}{y^3}{z^2} - 3{x^2}z + 2y - 14{x^3}{y^3}{z^2} + 6{x^2}z\)
\( = - 7{x^3}{y^3}{z^2} + 3{x^2}z\).
Khi đó, đa thức \[A\] hạng tử tự do là 0. Do đó ý c) sai.
⦁ Ta có \[A + G = \left( { - 7{x^3}{y^3}{z^2} + 3{x^2}z} \right) + \left( {7{x^3}{y^3}{z^2} - 3{x^2}z + 2y} \right)\]
\[ = - 7{x^3}{y^3}{z^2} + 3{x^2}z + 7{x^3}{y^3}{z^2} - 3{x^2}z + 2y\]
\[ = \left( { - 7{x^3}{y^3}{z^2} + 7{x^3}{y^3}{z^2}} \right) + \left( {3{x^2}z - 3{x^2}z} \right) + 2y\]\( = 2y\).
Như vậy, tổng của hai đa thức \[A\] và \(G\) là một đơn thức. Do đó ý d) đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp số: 73.
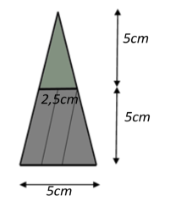
Thể tích của lọ nước hoa hình kim tự tháp là: \[{V_1} = \frac{1}{3} \cdot {5^2} \cdot 10 = \frac{{250}}{3}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\]
Thể tích của nắp lọ nước hoa là: \[{V_2} = \frac{1}{3} \cdot 2,{5^2} \cdot 5 = \frac{{125}}{{12}}\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\]
Dung tích của lọ nước hoa đó là: \(\frac{{250}}{3} - \frac{{125}}{{12}} \approx 73\;\;\left( {{\rm{c}}{{\rm{m}}^3}} \right) = 73\,\,\left( {{\rm{ml}}} \right)\).
Vậy dung tích của lọ nước hoa đó là \(73\,\,{\rm{ml}}.\)
Lời giải
Hướng dẫn giải
Đáp số: 35.
Xét tứ giác \[MNPQ,\] ta có: \(\widehat Q + \widehat {QMN} + \widehat N + \widehat {NPQ} = 360^\circ \) (tổng các góc của một tứ giác).
Suy ra \(\widehat {NPQ} = 360^\circ - \left( {\widehat {QMN} + \widehat N + \widehat Q} \right) = 360^\circ - \left( {110^\circ + 120^\circ + 60^\circ } \right) = 70^\circ \).
Do \[PM\] là tia phân giác của góc \[NPQ\] nên ta có: \(\widehat {MPQ} = \frac{{\widehat {NPQ}}}{2} = \frac{{70^\circ }}{2} = 35^\circ \).
Vậy số đo của \(\widehat {MPQ}\) là \(35^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo