Cho tam giác \(ABC\) có đường cao \(AH\). Kẻ \(HE \bot AB\) tại \(E\) kéo dài lấy \(ME = HE\). Kẻ \(HF \bot AC\) tại \(F\), kéo dài \(HF\) lấy \(FN = FH\). Gọi \(I\) là trung điểm của \(MN\).
a) \(AB\) là trung trực của \(NH.\)
b) \(EF\parallel MN.\)
c) \(\Delta AMN\) cân tại \(M.\)
d) \(AI \bot EF.\)
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án:
a) Sai.
b) Đúng.
c) Sai.
d) Đúng.
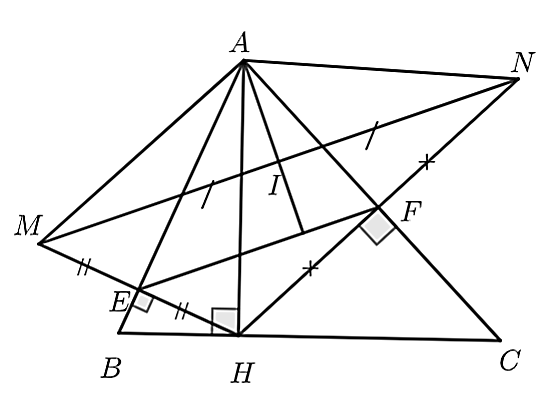
⦁ Ta có \(HE \bot AB\) tại \(E\) và \(ME = EH\).
Do đó, \(AB\) là trung trực của \(MH.\)
Lại có \(HF \bot AC\) tại \(F\) và \(FN = FH\).
Như vậy, \(AC\) là trung trực của \(NH.\) Do đó ý a) sai.
⦁ Xét tam giác \(MHN\) có \(E\) là trung điểm của \(MH\) và \(F\) là trung điểm của \(HN.\)
Do đó, \(EF\) là đường trung bình của tam giác \(HNM\).
Suy ra \(EF\parallel MN.\) Do đó ý b) đúng.
⦁ Xét \(\Delta EAH\) và \(\Delta EAM\) có: \(AE\) chung; \(ME = EH\) nên \(\Delta EAH = \Delta EAM\) (hai cạnh góc vuông)
Suy ra \(AM = AH\) (hai cạnh tương ứng).(1)
Tương tự, ta chứng minh \(\Delta FAH = \Delta FAN\) (hai cạnh góc vuông)
Suy ra \(AN = AH\) (hai cạnh tương ứng.(2)
Từ (1) và (2) suy ra \(AM = AN\) nên tam giác \(AMN\) cân tại \(A.\) Do đó ý c) sai.
⦁ Vì \(I\) là trung điểm của \(MN\) mà tam giác \(AMN\) cân tại \(A\) nên\(AI\) là đường cao của \(\Delta AMN.\)
Mà \(EF\parallel MN\) (cmt) nên \(AI \bot EF.\) Do đó ý d) đúng.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
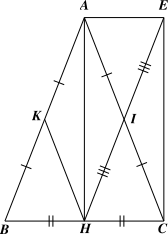
a) Xét
\(\Delta ABC\) cân tại \(A\) có \(AH\) là đường trung tuyến nên đồng thời là đường cao của tam giác.
Do đó \(AH \bot BC\) nên \(\Delta AHB\) và \(\Delta AHC\) đều vuông tại \(H.\)
Xét \(\Delta AHB\) vuông tại \(H\) có \(HK\) là đường trung tuyến ứng với cạnh huyền \(AB\) nên \(KH = \frac{1}{2}AB\) (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông).
Tương tự, xét \(\Delta AHC\) vuông tại \(H\) ta có \(IH = \frac{1}{2}AC.\)
Mà \(I,\) \(K\) lần lượt là trung điểm của \(AC\) và \(AB\) nên \[KA = KB = \frac{1}{2}AB;\,\,IA = IC = \frac{1}{2}AC.\]
Lại có \(AB = AC\) (do \(\Delta ABC\) cân tại \(A)\) nên \(KA = KH = IA = IH.\)
Xét tứ giác \(AKHI\) có \(KA = KH = IA = IH\) nên là hình thoi.
b) Xét tứ giác \(AHCE\) có \(I\) là trung điểm của hai đường chéo \(AC,\,\,HE\) nên \(AHCE\) là hình bình hành.
Lại có \(\widehat {AHC} = 90^\circ \) nên hình bình hành \(AHCE\) là hình chữ nhật.
Để hình chữ nhật \(AHCE\) là hình vuông thì hai cạnh kề bằng nhau, tức \(HA = HC.\)
Mà \(H\) là trung điểm của \(BC\) nên \(HB = HC = \frac{1}{2}BC.\)
Khi đó \[HA = HB = HC = \frac{1}{2}BC.\]
Xét \(\Delta ABC\) có đường trung tuyến \(AH\) thỏa mãn \[HA = \frac{1}{2}BC\] nên \(\Delta ABC\) vuông tại \(A.\)
Vậy \(\Delta ABC\) vuông cân tại \(A\) thì \(AHCE\) là hình vuông.
Câu 2
A. \[92,25\% \].
B. \(52,25\% \).
C. \(7,75\% \).
D. \(72,75\% \).
Lời giải
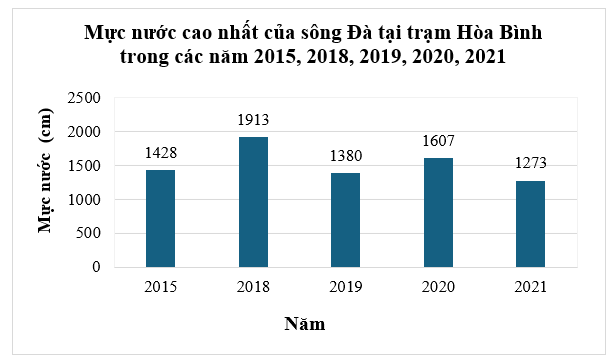
Tỉ lệ phần trăm mực nước cao nhất của sông Đà tại trạm Hòa Bình năm 2021 so với năm 2019 là:
\[\frac{{1{\rm{ }}273}}{{1{\rm{ }}380}}.100\% \approx 92,25\% \]
Do đó, năm 2021 mực nước cao nhất của sông Đà tại trạm Hòa Bình đã giảm \[100\% - 92,25\% = 7,75\% \] so với năm 2019.
Câu 3
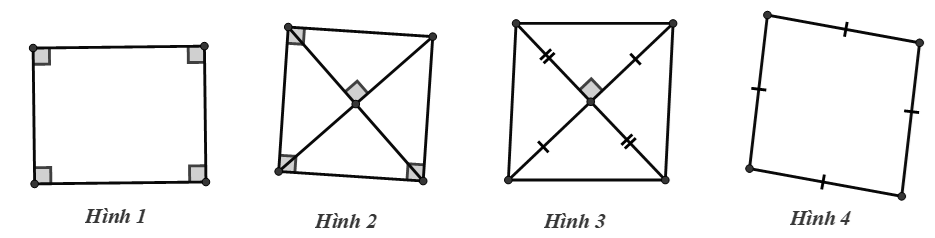
A. Hình 1.
B. Hình 2.
C. Hình 3.
D. Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
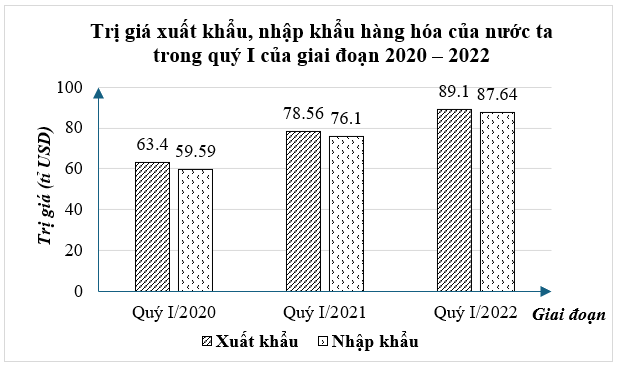
A. Biểu đồ đoạn thẳng.
B. Biểu đồ cột kép.
C. Biểu đồ tranh.
D. Biểu đồ hình quạt tròn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.