Cho hai đa thức:
\[R = \left( {xy - 4{x^2} + 2} \right) \cdot x{y^2}\] và \[T = \left( {15{x^3}{y^4} - 20{x^4}{y^3} + 10{x^2}{y^3}} \right):5xy.\]
Đa thức \(S\) thỏa mãn \(R = T - S.\)
a) Hệ số tự do của đa thức \(R\) là 2.
b) Bậc của đa thức \(T\) là 3.
c) Giá trị của biểu thức \(T\) tại \[x = 1\,;\,\,y = - 1\] là \( - 5\).
d) \(S\) là một đơn thức.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án:
a) Sai.
b) Sai.
c) Đúng.
d) Đúng.
⦁ Ta có \[R = \left( {xy - 4{x^2} + 2} \right) \cdot x{y^2}\]
\( = xy \cdot x{y^2} - 4{x^2} \cdot x{y^2} + 2 \cdot x{y^2}\)\( = {x^2}{y^3} - 4{x^3}{y^2} + 2x{y^2}\).
Khi đó, hệ số tự do của đa thức \[R\] có bậc là 2. Do đó ý a) sai.
⦁ Ta có \[T = \left( {15{x^3}{y^4} - 20{x^4}{y^3} + 10{x^2}{y^3}} \right):5xy.\]
\( = 15{x^3}{y^4}:\left( {5xy} \right) - 20{x^4}{y^3}:\left( {5xy} \right) + 10{x^2}{y^3}:\left( {5xy} \right)\)
\( = 3{x^2}{y^3} - 4{x^3}{y^2} + 2x{y^2}.\)
Khi đó, bậc của đa thức \(T\) là 5. Do đó ý b) sai.
⦁ Thay \[x = 1\,;\,\,y = - 1\] vào biểu thức \(T\), ta có:
\(T = 3 \cdot {1^2} \cdot {\left( { - 1} \right)^3} - 4 \cdot {1^3} \cdot {\left( { - 1} \right)^2} + 2 \cdot 1 \cdot {\left( { - 1} \right)^2} = - 3 - 4 + 2 = - 5.\)
Vậy với \[x = 1\,;\,\,y = - 1\] thì \(T = - 5\). Do đó ý c) đúng.
⦁ Ta có \(R = T - S\)
Suy ra \(S = T - R\)
\( = \left( {3{x^2}{y^3} - 4{x^3}{y^2} + 2x{y^2}} \right) - \left( {{x^2}{y^3} - 4{x^3}{y^2} + 2x{y^2}} \right)\)
\( = 3{x^2}{y^3} - 4{x^3}{y^2} + 2x{y^2} - {x^2}{y^3} + 4{x^3}{y^2} - 2x{y^2}\)
\( = \left( {3{x^2}{y^3} - {x^2}{y^3}} \right) + \left( { - 4{x^3}{y^2} + 4{x^3}{y^2}} \right) + \left( {2x{y^2} - 2x{y^2}} \right)\)\( = 2{x^2}{y^3}.\)
Như vậy, \(S\) là một đơn thức. Do đó ý d) đúng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án:
a) Đúng
b) Sai.
c) Sai.
d) Đúng.
⦁ Tứ giác \(BMND\) có: \[MN\parallel BD{\rm{ }}\left( {MN\parallel BC} \right)\]; \[MN = BD\] (gt).
Do đó, tứ giác \(BMND\)là hình bình hành. Do đó ý a) là đúng.
⦁ Vì \(\Delta {\rm{ }}ABH\) vuông tại \(H\,\,\left( {AH \bot BC} \right)\) có \(HM\) là trung tuyến nên \(HM = \frac{1}{2}AB\).
Mà \(MA = \frac{1}{2}AB\) suy ra \(MA = HM\).
Vậy \(\Delta {\rm{ }}AMH\) cân tại \[M\]. Do đó ý b) sai.
⦁ Tứ giác \(DHMN\) có \[MN\parallel DH{\rm{ }}\left( {MN\parallel BC} \right)\] nên tứ giác \(DHMN\) là hình thang.\(\left( 1 \right)\)
Ta có \(AH \bot BC\); \[MN\parallel BC\] nên \(AH \bot MN\).
Vì \(\Delta {\rm{ }}AMH\) cân tại \[M\] có \(AH \bot MN\) nên \(MN\) là phân giác của \(\Delta {\rm{ }}AMH\).
Do đó \(\widehat {AMN} = \widehat {HMN}.\) Do đó ý c) sai.
⦁ Tứ giác \(BMND\)là hình bình hành nên \[ND\parallel MB\].
Do đó \(\widehat {AMN} = \widehat {DNM}\)(so le trong) nên \(\widehat {HMN} = \widehat {DNM}\).\(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra tứ giác \(DHMN\) là hình thang cân. Do đó ý d) đúng.
Lời giải
Đáp án đúng là: C
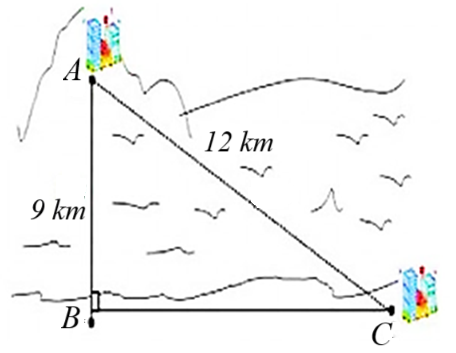
Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\)
Suy ra \(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {{{12}^2} - {9^2}} = \sqrt {63} \) (km).
Chi phí làm đường ống từ \(B\) tới điểm \(C\) của công ty trên bằng tiền VNĐ là:
\(\sqrt {63} \cdot 5\,\,000 \cdot 26\,\,115 = 1\,\,036\,\,406\,\,932\) (đồng) \( \approx 1,036\) (tỉ đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo